2024 ICPC Asia Pacific Championship 후기

서론

지난 2월 29일부터 3월 3일까지 베트남 하노이에서 열린 2024 ICPC Asia Pacific Championship에 참가했습니다. 관광은 별로 관심이 없어서 따로 기록하진 않았고, 대회 이야기를 해 보려고 합니다. 2023 ICPC Asia Seoul Regional Contest 후기(링크)에서 이어지는 글입니다. 팀원 구성과 팀 특성 같은 내용은 서울 리저널 후기에서 확인할 수 있습니다.

대회 소개

ICPC는 한국이 속한 Asia Pacific을 포함해 Asia East, Asia West, South Pacific, Norhern Eurasia, Europe, North America, Latin America, Africa 등 여러 개의 슈퍼 리저널로 분할되어 있고, 각 슈퍼 리저널에서 독자적인 규칙을 통해 월드 파이널 진출 팀을 선정합니다. Asia Pacific 지역은 지난 2022-2023 cycle까지 각 리저널 대회 상위 2~3팀을 선발했고, 다른 모든 지역은 리저널 대회 상위 팀들을 모아서 지역 챔피언십을 개최해 월드 파이널 진출 팀을 선발했었습니다. 그리고 올해, 2023-2024 cycle부터 Asia Pacific 지역도 챔피언십 대회가 신설되었습니다.

ICPC Asia Pacific Championship(이하 플레이오프)은 2019년부터 이야기가 나왔었지만(링크), 코로나 19(아마도?)로 인해 계속 미뤄지다가 이번 2023-2024 cycle에 처음으로 개최되었습니다. 각 리저널 대회(Seoul, Yokohama, Jakarta, Taoyuan, Hue city)에서 우승한 5팀은 월드 파이널에 직행하고, 나머지 진출권은 이번 대회를 통해 결정하는 방식입니다. 리저널 우승팀이 소속된 대학은 우승팀만, 다른 대학에서는 최대 3팀이 플레이오프에 진출할 수 있습니다. 각각 한국 대회와 베트남 대회에서 우승한 카이스트 Penguins팀과 서울대학교 NewTrend팀 덕분에 한국에서는 매우 다양한 대학의 팀이 플레이오프에 진출하게 되었습니다. 인도네시아 대회에서 티켓을 뺏어온 서강대학교 Redshift팀과 전북대학교 2 3 5 8 14팀도 한국 진출 팀을 늘리는 데 큰 역할을 했습니다. 65팀 중 14팀이 한국 팀이었습니다.

한국에서 여러 팀이 진출한 만큼 재미있는 후기 글도 많이 올라왔습니다. 함께 보시면 좋을 것 같습니다.

포스텍 AllSolvedin1557팀 leo020630님 후기 #1, #2, #3
포스텍 AllSolvedin1557팀 kwoncycle님 후기 #
연세대 SCC_SinChonCoders팀 ystaeyoon113님 후기 #
연세대 cookie팀 plast님 후기 #

우리 연습 진짜 안 해?

서울 리저널 전까지는 시간 날 때마다 팀 연습을 했었습니다. 2023년 말 ~ 2024년 초는 저와 kyo20111가 Good Bye, BOJ 2023!, Hello, BOJ 2024! 개최 준비를 하고 있었던 상황이라 두 대회가 모두 끝나고 1월 중순부터 팀 연습을 다시 시작하려고 했지만… 저는 갑자기 네이버 인턴(기습 홍보)에 합격해 버려서 연습할 시간이 없었고, 다른 두 팀원도 회사와 해외여행 때문에 시간이 없어서 단 한 번도 연습을 진행하지 않았습니다. 팀 연습만 하지 않은 게 아니라 아예 3명 모두 PS에 시간을 투자하지 못해서 2월 말이 됐을 때는 살짝 맛이 가 있는 상태였습니다. 풀이도 바로바로 안 나오고 코딩 실수도 많이 하고…

230701(토) UCPC 2023 예선 (3시간)
230722(토) UCPC 2023 본선 (5시간)
231011(수) ECNA 2022 (3시간)
231012(목) TOPC 2023 (3시간)
231013(금) SWERC 2016 (5시간)
231016(월) Brazil 2023 (3시간)
231021(토) 2023 ICPC 서울 지역 대회 예선 (3시간)
231027(금) 2023 Latin (5시간)
231029(일) 2023 Macau (5시간)
231106(월) NCPC 2021 (5시간)
231120(월) 2023 CCPC Guilin (5시간)
231122(수) CERC 2020 (5시간)
231125(토) 2023 ICPC 서울 지역 대회 본선 (5시간)

(공백)

240302(토) 2024 ICPC Asia Pacific Championship (5시간)

팀노트 작업

ICPC 대회에 참가할 때마다 항상 더 이상 추가할 내용이 없을 것이라 생각하면서 팀노트 작업을 마감하고 있습니다. 하지만 주기적으로 이상한 알고리즘을 새로 배워오는 사람들 덕분에 매번 기존 코드의 길이를 줄이고 필요 없는 내용을 쳐내서 공간을 만든 다음에 새로 공부한 것을 넣는 행동을 반복하고 있습니다. 이게 진짜 힘든데… 아무도 안 알아줍니다.

지금까지 주로 준비했던 ICPC 서울 리저널 대회는 2n년 간의 기출 문제를 기반으로 정수론, 다항식, 생성 함수, 3차원 기하 등 꽤 많은 분야를 배제하고 준비할 수 있었지만, 이번에 참가하는 ICPC Asia Pacific Championship은 올해 처음으로 개최되는 대회이기 때문에 어떠한 것도 배제하면 안 된다고 생각했습니다. 특히 이번 대회의 scientific committee(명단)에 베트남 사람이 2명이나 있는 것이 많이 신경 쓰였습니다. 베트남은 지난 몇 년 동안 리저널 대회에 생성 함수 문제를 출제한 전적이 있으므로 이번에도 무조건 생성 함수 문제가 나올 것으로 생각했고, 팀노트의 꽤 많은 지면을 조합론 카운팅과 다항식 관련 라이브러리에 투자했습니다. 이 밖에도 대회 환경을 알 수 없으므로 스택 사이즈 제한을 우회하는 이상한 인라인 어셈블리 코드, 왠지 나만 빼고 다 알고 있는 것만 같은 각종 transform/convolution 코드도 추가했습니다. 3차원 기하는 팀에 다룰 줄 아는 사람이 없으므로 과감하게 포기했습니다. 수십 개의 팀노트를 모두 보면서 3차원 기하와 선형 대수를 제외한 내용은 모두 넣은 것으로 기억합니다. 작업 내용은 다음과 같습니다.

수학
- 카운팅, 생성 함수, Faulhaber 공식 관련 노트 추가
- $O(n \log n)$ polynomial log 추가
- $O(n \log n)$ polynomial exp 추가
- $O(n \log n)$ polynomial pow 추가
- $O(n \log n)$ polynomial sqrt 추가
- $O(n \log n)$ polynomial sampling shift 추가
- zeta/mobius transform, and/or/gcd/lcm convolution 추가
- primitive root finder 추가
- $O(n \log^2 n)$ multipoint evaluation 코드 길이 단축
- $O(n \log^2 n)$ polynomial interpolation 코드 길이 단축
- 행렬, 다항식 관련 알고리즘의 실제 실행 시간 표기
기하
- $O(n^2)$ 원 합집합 넓이 추가
그래프
- degree sequence 관련 노트 추가
- lr flow, circulation, cost-scaling mcmf 추가
- directed mst 코드 길이 단축
문자열
- all lcs 추가
기타
- stack hack 추가
- 각종 bithack 추가

팀노트는 아마 9월에 개최되는 2024 ICPC 월드 파이널이 끝난 다음에 공개할 것 같습니다.

목표와 경쟁 상대

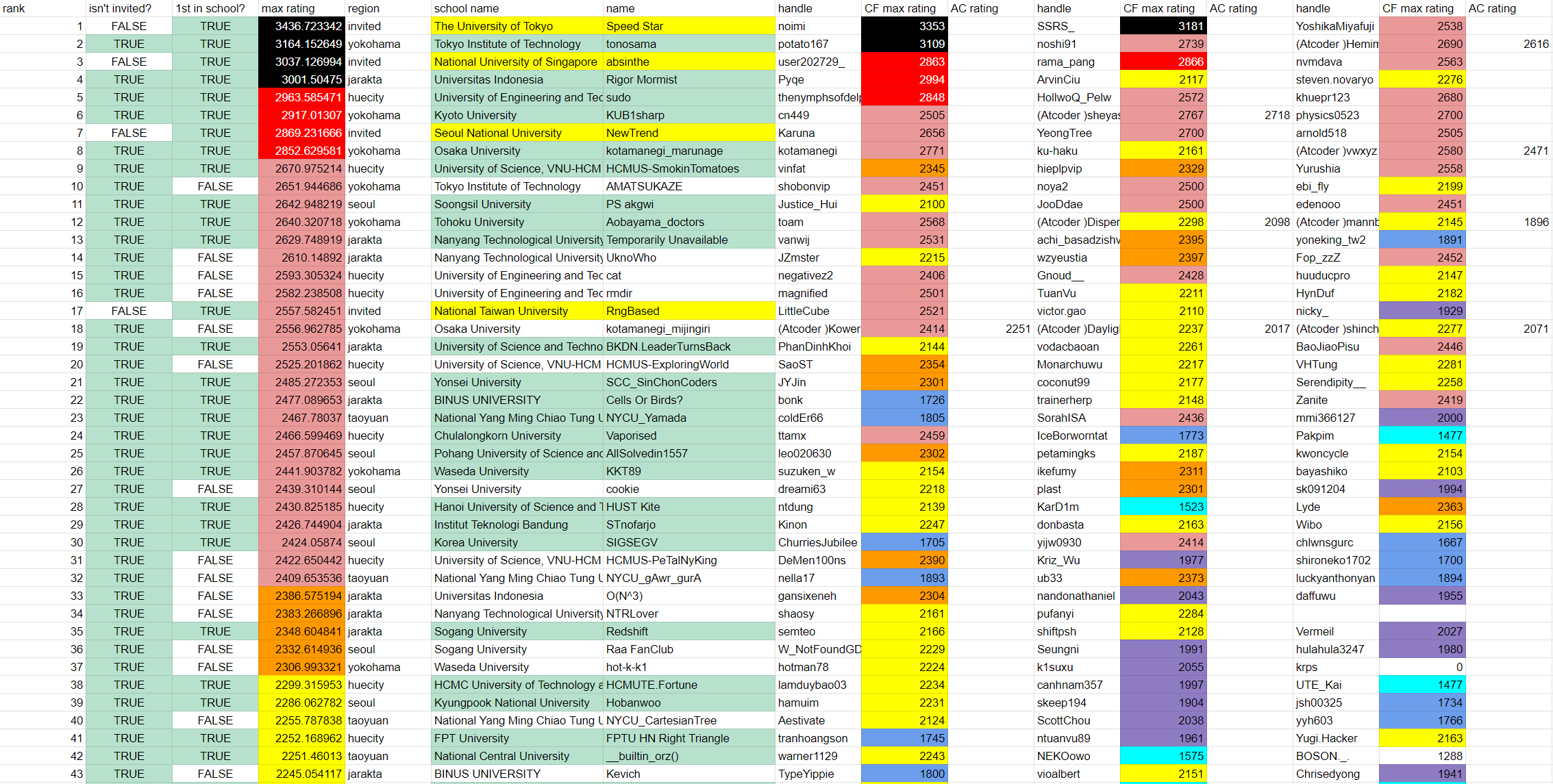
가장 중요한, 그리고 유일한 목표는 월드 파이널 진출입니다. edenooo는 지난 학기를 끝으로 졸업했기 때문에 이번이 마지막 기회였고, 숭실대에는 edenooo의 역할을 대신할 수 있는 사람은 없기 때문에 다른 2명(jhnah917, kyo20111)도 이번이 마지막이라 생각하고 대회에 임했습니다. 서울 리저널 대회를 치르던 11월의 실력으로는 WF 진출권을 따지 못하는 게 불가능하다고 생각했지만, 이번 대회는 팀원 3명의 상태가 모두 별로 좋지 않아서 걱정을 많이 했었습니다. 마침 코드포스에 Teams going to the 2024 ICPC Asia Pacific Championship(링크)라는 글이 올라왔길래 참가자들의 레이팅을 확인해 봤는데…

어…

일단 SpeedStar(TokyoU), absinthe(NUS), NewTrend(SNU), RngBased(NTU)와 시트에 없는 Penguins(KAIST)는 리저널 우승 팀이기 때문에 이미 WF 진출이 확정된 상태였습니다. 아시아 태평양 지역에는 보통 WF 티켓이 16장 정도 할당되기 때문에 WF 진출이 확정된 팀을 제외하고 대학 순위 기준 11등 안에 들어야 했습니다. 위에 있는 시트를 보면서 우리 팀이 질 수도 있다는 생각이 드는 팀(볼드체는 리저널 우승팀)은 다음과 같았습니다.

한국(2팀): 서울대, 카이스트
일본(4팀): 도쿄대, 교토대, 도쿄공대, 오사카대
싱가포르(2팀): NUS, 난양공대
대만(1팀): NTU
인도네시아(1팀): 인도네시아대학
베트남(2팀): VNU-HCM, VNU-UET

이 팀들에게 다 져도 16등 안에는 들 수 있기 때문에 말리지만 않는다면 WF 진출은 가능할 것으로 예상했습니다.

예비 소집

잘 치고 싶은 대회는 항상 긴장되고, 잘 치는 것이 당연한 대회도 잘 하지 못할까 봐 항상 떨립니다. 이번 대회는 그 둘 모두 해당하는 대회라서 인천 공항에서부터 정말 많이 긴장하고 있었고, 다른 팀들의 실력을 처음으로 확인할 수 있는 예비 소집 날은 말 그대로 다리가 덜덜 떨리고 있었습니다.

예비 소집 문제는 12개였지만, 문제 번호를 4로 나눈 나머지가 같은 문제는 같은 문제였기 때문에 실제로는 4문제였습니다. edenooo는 다른 일정이 있어서 예비 소집이 끝날 때쯤 대회장에 도착했었기 때문에 예비 소집은 저와 kyo20111 2인팀으로 참가했습니다. 문제 지문만 읽었을 때의 첫인상은 다음과 같았습니다.

A. rope 쓰면 바로 풀 수 있는 문제 → __gnu_cxx::crope 사용법 까먹어서 1번 틀린 다음에 AC
B. 애드혹?
C. 안 읽었는데 kyo20111이 쉽다면서 풀었음
D. 쉬운 문제 → 실수 오차 때문에 2번 틀린 다음에 AC

B는 머리를 써야 하는 문제 같아서 kyo20111에게 던져두고 저는 손가락만 움직이면 되는 A와 D를 풀었습니다. 제가 A D를 구현하는 동안 kyo20111이 50 이하의 소수가 15개밖에 없다는 것을 이용하면 될 것 같다는 관찰을 했고, 저는 15를 보자마자 Bit DP를 외치며 키보드를 잡았습니다. 전형적인 Bit DP라서 풀이 구체화는 빠르게 할 수 있었고, 사소한 부분을 하나 놓쳐서 1번 틀리고 AC를 받았습니다.

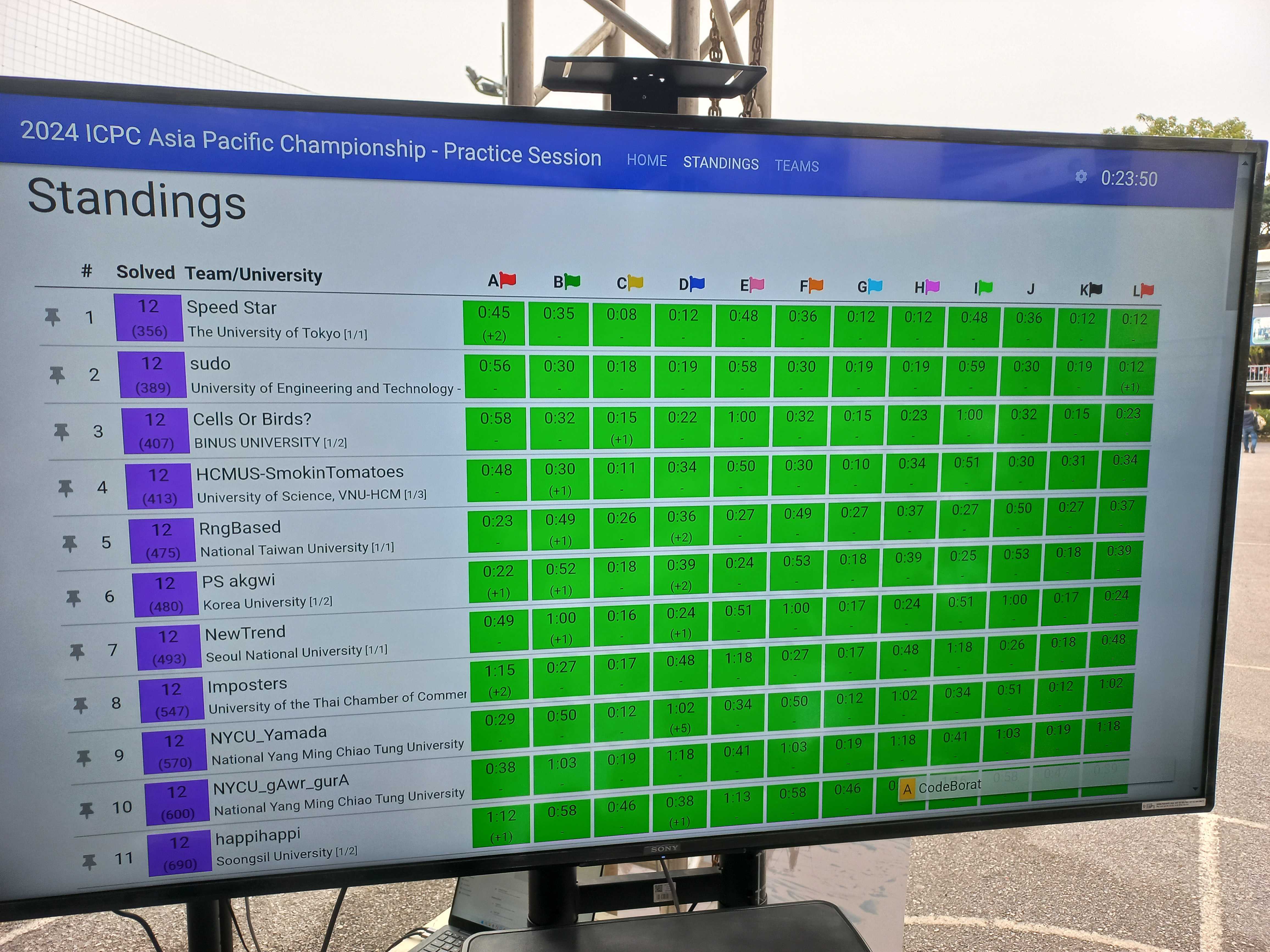
예비 소집은 6등으로 마무리되었습니다. 예상했던 것보다 훨씬 높은 등수를 받은 것을 보며 해외 팀들이 그렇게 잘하지 않는다는 것을 깨달았습니다. 대회 초반에 말리더라도 어떻게든 복구해서 월드 파이널에는 진출할 수 있을 것이라는 자신감이 생겼고, 실제로 예비 소집이 끝난 뒤에는 이전처럼 별로 긴장이 되지 않았습니다.

대회

드디어 결전의 날입니다. 이제야 이야기하는 건데, 사실 PS akgwi 팀은 팀 전략이 없습니다. 유일하게 지키는 원칙은 대회 시작하고 1시간 안에 모든 사람이 모든 문제의 내용을 알고 있기? 정도밖에 없습니다. 기하랑 문자열은 제가 잡고, 경우의 수 구해야 하면 edenooo한테 주고, 머리 써야 하는(내가 풀기 싫은) 문제나 든든한 국밥 같은 문제는 kyo20111 주고, 안 풀리면 서로 바꿔서 보고… 기본적으로 서로를 믿을 수 있을 정도로 실력이 좋고, 3명의 강점이 서로 다르기 때문에 한 명이 말려도 나머지 2명이 커버할 수 있는 조합이라서 가능한 방법인 것 같습니다. 2022년 서울 리저널에 참가했던 NLP 팀은 팀 전략이 확실히 있었기 때문에 후기(링크)에 대회 진행 상황을 열심히 적었는데, 이번 대회는 2023 서울 리저널과 마찬가지로 별로 기억나는 것이 없습니다. 그래서 그냥 제가 푼 문제(B, C, H) 풀이만 간단하게 적어보려고 합니다.

H. Pho Restaurant (BOJ 31600)

2가지의 메뉴만 판매하는 식당에 $N$개의 테이블이 있다. $i$번째 테이블에 $\vert S_i \vert$명의 사람이 있고, $i$번째 테이블의 $j$번째 사람은 $S_i[j]$번 메뉴를 주문하려고 한다. 식당 주인은 주문 처리의 편의를 위해, 사람을 몇 명의 사람을 다른 테이블로 옮겨서 같은 테이블에 있는 사람은 모두 같은 음식을 주문하도록 만들려고 한다. 이때 필요한 사람 이동 횟수의 최솟값을 구하는 문제
$N \leq 100\,000;$ $1 \leq \sum \vert S_i\vert \leq 200\,000$

대회에서 가장 먼저 풀린 문제입니다. 쉬운 문제였지만 스코어보드에 불기둥이 세워지고 있던 상태라 정신 똑바로 차리고 문제를 잡았습니다.

$S_i$에서 $0$의 개수를 $C(i, 0)$, $1$의 개수를 $C(i, 1)$이라고 합시다. 일반적으로는 $C(i, 0) < C(i, 1)$이면 $0$번 메뉴를 주문한 사람, 반대의 경우에는 $1$번 메뉴를 주문한 사람을 옮기는 것이 좋을 것 같지만, 이게 정답이었으면 스코어보드에 불기둥이 세워지진 않았을 것 같아서 코너 케이스를 고민하기 시작했습니다.

$N$개의 테이블에서 모두 $C(i, 0) < C(i, 1)$이라면 $S_i[j] = 0$인 사람만 옮기려고 할 텐데, 테이블을 새로 추가할 수는 없기 때문에 이 사람들이 갈 수 있는 곳이 없습니다. 따라서 이런 상황에서는 $C(i, 1) - C(i, 0)$이 가장 작은 테이블로 $S_i[j] = 0$인 사람을 모아야 하고, 이 케이스만 잘 처리하면 AC를 받을 수 있습니다.

C. Bit Counting Sequence (BOJ 31595)

음이 아닌 정수 $x$를 이진법으로 표현했을 때 등장하는 1의 개수를 $p(x)$라고 정의하자. 수열 $A_1, A_2, \cdots, A_N$이 주어지면 $p(x), p(x+1), \cdots, p(x+N-1)$이 $A$와 같은 가장 작은 $x$를 구하는 문제
$T \leq 1\,000;$ $N \leq 500\,000;$ $0 \leq A_i \leq 60$

문제를 처음 봤을 때의 관상은 “내가 못 푸는 문제”였습니다. 하늘에서 뚝 떨어진 뜬금없는 아이디어 하나 잡고 이리저리 고민해서 풀어야 할 것만 같은, 제가 별로 안 좋아하는 유형의 문제처럼 보였습니다.

사실 문제를 푼 방법도 이것과 크게 다르지 않습니다. $\min A_i = 1$이면 쉽게 풀 수 있다는 것만 관찰하고 풀이가 보이지 않아서 멍때리고 있었는데, 뜬금없이 rkm0959의 얼굴이 떠오르더니 rkm0959가 BOJ 13729번 문제(링크)에 난이도 투표에 남긴 “믿음을 가지고 lifting”이라는 문장이 생각났습니다.

뜬금없이 튀어나온 “lifting”이라는 단어는 하늘이 점지해 준 것이 분명해 보였습니다. 이 키워드를 갖고 열심히 고민한 결과, 다음과 같이 그럴듯한 가설을 만들어낼 수 있었습니다.

$A_1, A_2, \cdots, A_N$의 정답을 $x$라고 하면, $A_1+1, A_2+1, \cdots, A_N+1$의 정답은 $x + 2^{\lfloor log_2 (x+N-1) \rfloor + 1}$이다.

즉, $x+N-1$의 최상위 비트보다 한 칸 더 높은 비트를 켠 것이 $A_1+1, A_2+1, \cdots, A_N+1$의 정답이라는 것입니다. 이 가설이 참이라면 $A$의 모든 원소에 $\min A_i - 1$를 빼서 $\min A_i = 1$인 문제를 해결한 뒤, 적당히 “lifting” 시키는 것으로 전체 문제를 해결할 수 있습니다! 예제를 보니 대충 맞는 것 같아서 랜덤 스트레스 테스트를 돌려봤는데 반례가 나오지 않았습니다. 맞는 풀이일 것이라는 확신이 들어서 자신감을 갖고(믿음을 갖고) 구현을 시작했고, 한 번에 AC를 받았습니다.

B. Attraction Score (BOJ 31594)

2차원 평면 위에 $N$개의 정점이 주어지고, 서로 교차하지 않는 “선분 형태”의 가중치 있는 무향 간선이 $M$개 주어진다. 정점 부분 집합 $S \subset V$의 가중치가 다음과 같이 계산될 때, 가중치의 최댓값을 구하는 문제.
(1) 만약 $a, b \in S$를 연결하는 간선이 있으면 그 간선의 가중치를 더함
(2) 간선으로 연결되지 않은 $a, b \in S$ 쌍의 개수를 $f(S)$라고 할 때, $-10^6 \times f(S)^2$를 더함
$N \leq 100\,000;$ $M \leq 300\,000;$ $w \leq 10^6$

입력으로 주어지는 그래프는 평면 그래프입니다. 평면 그래프와 관련해서 다음과 같은 사실이 잘 알려져 있습니다.

평면 그래프는 4개의 색으로 칠할 수 있음 → 크기가 5 이상인 클리크가 존재하지 않음
$ V \geq 3$인 단순 평면 그래프는 항상 $E \leq 3V-6$을 만족함 → $2E < 6V$이므로 항상 차수가 5 이하인 정점이 존재함
perfect elimination ordering을 구하는 것과 비슷한 느낌으로, 차수가 작은 정점부터 차례대로 제거하면 $O(n)$개의 클리크를 모두 $O(n \log n)$ 시간에 구할 수 있음

일단, 간선이 하나 빠질 때마다 정점 집합 $S$의 가중치가 많이 감소합니다. 따라서 클리크에 가까운 형태만 보면 된다는 것은 쉽게 관찰할 수 있습니다. 실제로 간선이 2개 이상 빠지는 경우에는 가중치를 감소시키지 않으면서 차수가 $\vert S\vert -1$이 아닌 정점을 하나 지울 수 있습니다. 따라서 클리크와 간선이 하나 빠진 클리크만 고려해도 정답을 구할 수 있습니다. 평면 그래프는 $K_5$가 존재하지 않으므로 4개 이하의 정점으로 구성된 클리크, 5개 이하의 정점으로 구성된 간선 하나 빠진 클리크만 고려하면 됩니다.

클리크 찾아서 가중치 계산하는 건 쉬우니까 넘어가고, 간선이 하나 빠진 클리크를 잘 찾는 방법을 고민해야 합니다. $K_4$에서 간선을 하나 제거한 그래프는 삼각형($K_3$) 2개가 변 하나를 공유하고 있는 형태로만 등장할 수 있습니다. 따라서 각 간선마다 간선에 달려 있는 삼각형의 가중치를 모두 모은 다음, 가장 큰 2개를 보면 쉽게 해결할 수 있습니다.

이제 $K_5$에서 간선을 하나 제거한 형태만 찾으면 됩니다. 이 그래프는 간선이 항상 선분 형태라는 조건을 활용해야 합니다.

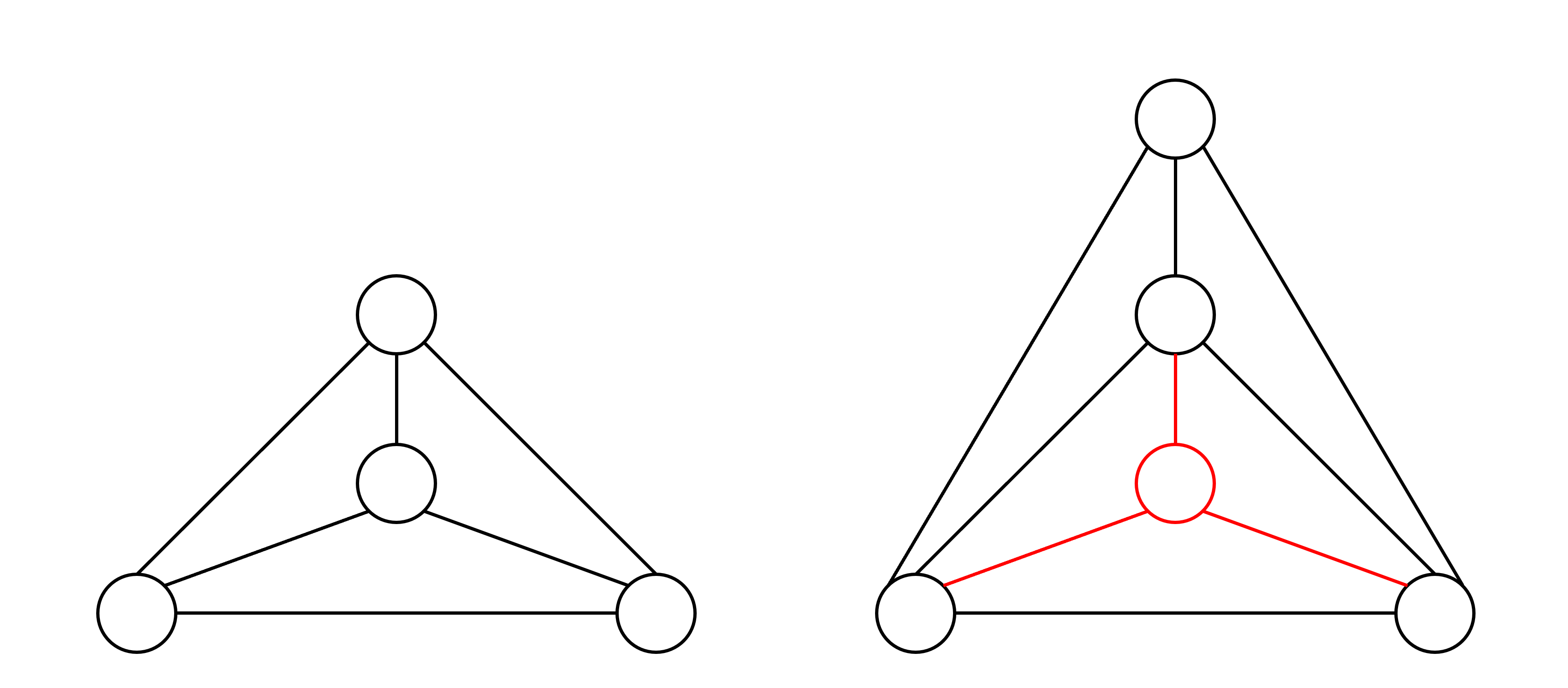
모든 간선이 선분 형태이기 때문에 $K_4$는 위 그림처럼 삼각형 안에 점이 하나 들어간 형태만 가능하고, 삼각형을 구성하는 점 3개가 고정되면 삼각형 내부에 클리크를 구성할 수 있는 점은 최대 1개만 존재합니다. 또한, $K_5$에서 간선이 하나 빠진 그래프는 위 그림처럼 $K_4$의 작은 삼각형 안에 $K_4$가 들어간 형태만 가능합니다. 따라서 $K_3$과 $K_4$를 다 구한 다음, 필요한 정보를 잘 뽑아서 정규화한 뒤, 전부 살펴보는 코드를 200줄 정도 작성하면 AC를 받을 수 있습니다.

저는 다음과 같은 구조체를 정의한 다음 열심히 구현했습니다. 아무튼 $O(n \log n)$에 되긴 합니다.

struct k3{
    array<int,3> v; // 정점 번호 오름차순 정렬
    array<int,3> e; // e[3-i-j] = v[i] v[j] 연결하는 간선 가중치
};

struct k4{
    k3 out; // 바깥쪽 삼각형
    array<k3,3> a; // 내부 점을 통해 만들어지는 삼각형
    array<int,3> in; // 안쪽 간선 3개 가중치
    array<int,3> out; // 바깥쪽 간선 3개 가중치
};

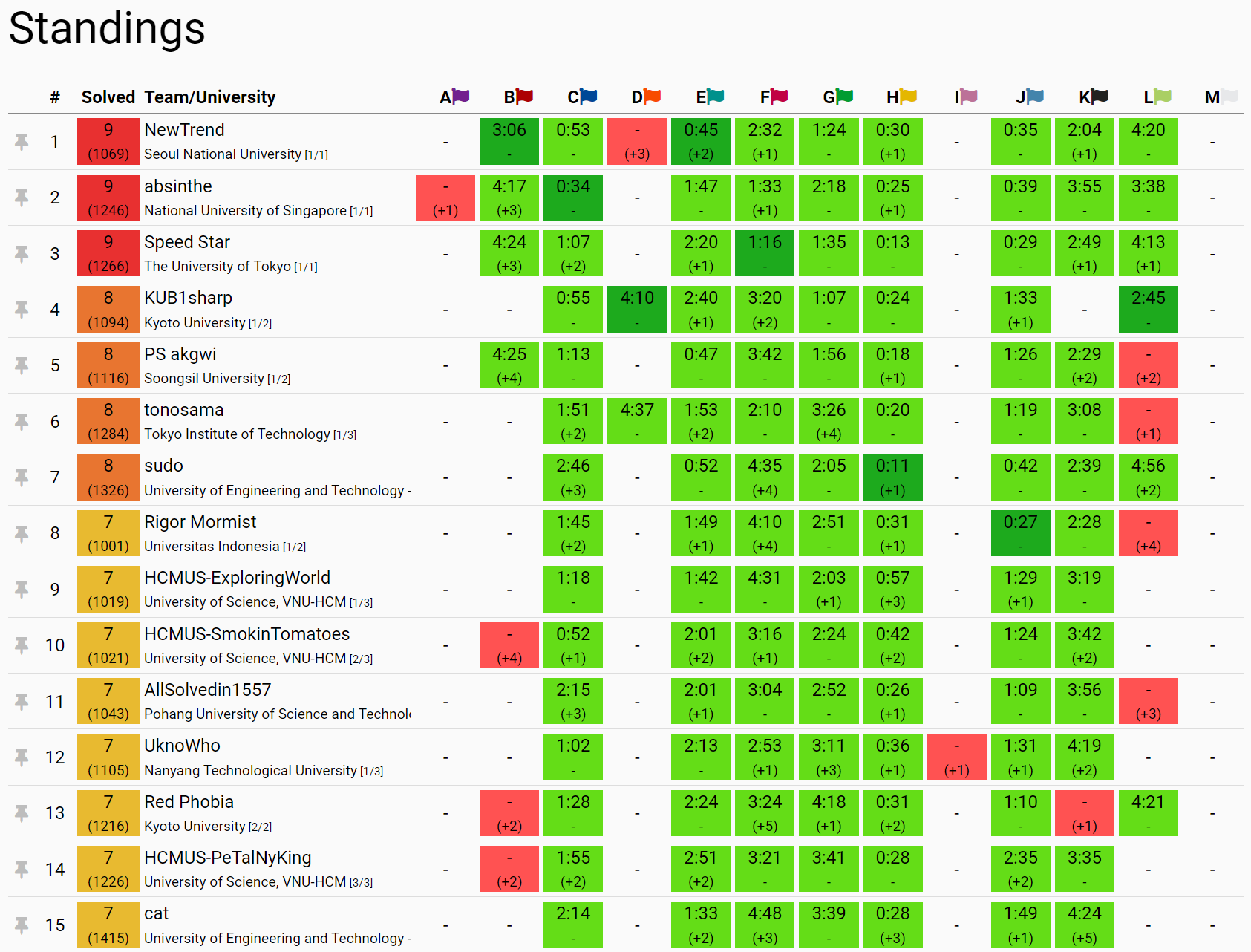
대회 결과

프리즈 전에는 4등이었지만 대회 마지막 1시간 동안 교토대학교가 D를 풀어서 5등으로 밀려났습니다. 처음에는 1n등 안에만 들어서 월드 파이널에 진출하는 것이 목표였지만, 막상 은메달 1등을 하고 나니 금메달을 못 받은 것이 아쉬웠습니다. 은탑 동탑은 그냥 한국의 전통인가…

한국에서는 리저널 대회 우승팀인 서울대학교 NewTrend, 카이스트 Penguins팀과 함께 이번 플레이오프에서 은메달을 받은 숭실대학교 PS akgwi, 포스텍 AllSolvedIn1557팀이 월드 파이널 진출을 확정 지었습니다. 유니스트 Potom팀과 연세대학교 SCC팀도 진출 가능성이 있어 보이는데 아직 아시아 태평양 지역에 티켓이 몇 장 떨어질지 몰라서… 빨리 발표되면 좋겠습니다.

SCCC의 미래

숭실대학교는 2020-2021 cycle부터 2023-2024 cycle까지 지난 4년 동안 ICPC에서 서울대학교와 카이스트, 그리고 2020년의 고려대학교를 제외하고는 적수가 없을 정도로 강력한 퍼포먼스를 보여주었습니다. 이런 실적은 같은 시기에 서로 분야가 다른 오렌지~레드급 실력자(18학번 aeren, 19학번 edenooo, 20학번 kyo20111, 21학번 jhnah917)가 학교에 3명 이상 있었고, 그 사람들이 모두 군대와 졸업을 미루면서까지 대회를 준비했었기에 가능했다고 생각합니다. 이번 대회를 끝으로 CF 오렌지 이상인 사람들은 모두 학교를 졸업하거나 월드 파이널 2회 진출자가 되어 더 이상 ICPC에 참가할 수 없게 되었습니다. 따라서 저를 포함한 많은 사람이 더 이상 숭실대에서 월드 파이널 진출 팀이 나오기는 어려울 것으로 예상하고 있었습니다.

하지만 이번 대회를 보면서 생각이 바뀌었습니다. 해외 팀들은 최상위권을 제외하면 생각했던 것만큼 강력하지 않았고, 팀원 조합을 잘 맞추고 연습을 열심히 한 2오렌지 1퍼플 팀이라면 월드 파이널 진출을 노릴 수 있을 것 같았습니다. 한국에서 3등 안에 드는 것은 어려운 일이지만 오렌지 2명 퍼플 1명이 나오는 건 가능해 보입니다. 저는 더 이상 ICPC에 나갈 수 없게 되었지만 아직 졸업까지 1년이라는 시간이 남아 있습니다. 1년 안에 민트~블루 정도 되는 사람들을 오렌지로 만드는 것은 힘들더라도, 함께 공부할 수 있는 환경을 만들기 위해 노력해 보려고 합니다. 제발 제가 숭실대의 마지막 월드 파이널 진출자가 아니길 바랍니다…

마무리

ICPC 온사이트 대회만 나가면 5등을 하는 사람이 되었습니다. 온라인으로 진행된 21 리저널을 제외하면 22 리저널과 23 리저널, 그리고 이번 24 플레이오프에서 모두 5등(은상)을 받았습니다. WF에서도 5등을 하면 참 좋을 텐데… 이건 진짜 어림도 없어 보입니다.

ICPC는 WF에 2번 진출해서 더 이상 참가하지 못하고, 1년 뒤면 대학교도 졸업하기 때문에 SCPC와 UCPC 같은 대학생 대회도 올해가 마지막 참가가 될 것 같습니다. 중고등학생 때 정보 올림피아드를 준비할 때부터 프로그래밍 대회는 항상 끝이 보이지 않는 레이스와 같은 느낌이었는데 드디어 끝이 보이기 시작했습니다. 반년만 더 열심히 공부해서 만족할 만한 성과를 거두고 아름답게 마무리하고 싶습니다.

다음 글은 (이집트 여행기에 더 가까운) 2023 ICPC WF 후기로 찾아오겠습니다. 왜 2023 ICPC WF가 아직도 안 열렸는지는 모르겠지만…