올해도 어김없이 대회를 열었습니다.
올해도 어김없이 대회를 열었습니다.
올해도 대회 하나요?
2019년 말 ‘Good Bye, BOJ 2019!’로 시작된 이 대회는 매년 연말연시에 개회(하는 것을 목표로)하는 행사입니다. 대회 운영 방식은 일단 9~10월에 사람을 모은 뒤, 한 명이 총대를 메고 행사 개최를 성사시키면, 나머지 사람들이 열심히 문제를 만들어서 대회를 성공적으로 마무리한 뒤, “내년에는 절대 하지 말자”라는 다짐과 함께 해산하는 식입니다. 대회 총대의 막중한 책임은 주로 leejseo와 ryute, 또는 당해 전대프연 회장이 번갈아 가면서 짊어지고 있습니다.
올해도 일단 사람을 불러 모은 뒤 나머지는 leejseo와 ryute가 준비할 것이라 믿고 별로 신경 쓰지 않고 있었습니다. 그러나 경기 침체로 인해 후원사 섭외에 어려움이 생겼고, 대회 개최가 불투명해졌습니다. 언젠가는 해결될 것이라 생각하고 기다렸지만 12월이 되어도 소식이 없자, 앞으로의 계획에 대한 진지한 고민에 빠졌습니다. 2019년처럼 소규모로 대회를 열고 친한 사람들끼리 뒷풀이 겸 신년회를 여는 방안이 가장 유력했습니다만…
극적으로 12월 말에 스타트링크에서 대회 후원 의사를 밝혀주셨습니다. 즉시 문제를 모으기 시작했고, 1월 중순부터는 본격적인 대회 준비에 돌입했습니다. 이 시점부터는 대회 개최에 대한 불안감은 사라졌습니다. 대회에 낼 문제 아이디어도 모두 모였고, 운영진 모두 크고 작은 대회를 이끌어 본 경험이 있었기에 문제 작업과 행정 처리 모두 원활하게 진행될 것이라 확신했습니다.
대회 준비 시작
다른 건 별로 걱정이 안 됐지만, 대회 일정과 장소, 그리고 오프라인 대회 초청 방법 때문에 고민이 많았었습니다.
‘Hello, BOJ’라는 이름에 걸맞게 1월 개최가 이상적이나, 오프라인 대회를 2주 만에 준비하는 것은 현실적으로 불가능했습니다. 게다가 2월 24일부터는 일부 학교(특히 카이스트)가 개강하므로, 2월 9일, 16일, 23일을 후보로 잡고 장소 대관이 가능한 가장 늦은 날짜로 결정하기로 했습니다. 대회 장소 역시 여러 후보를 검토했는데, 다행히도 작년 ‘Hello, BOJ 2024!’를 통해 인연을 맺은 LG전자에서 다시 한번 장소를 후원해 주시겠다고 했습니다. 덕분에 장소 확보와 대관 비용에 대한 걱정을 모두 덜 수 있었습니다.
지난 2년간은 온라인 대회인 ‘Good Bye, BOJ’ 대회를 통해 오프라인 대회 ‘Hello, BOJ’의 참가자를 선발했으나, 이번에는 1월부터 준비를 시작했기에 새로운 선발 방식이 필요했습니다. 이에 관한 내용은 뒤에서 다시 설명하겠습니다.
나의 역할
첫 대회를 운영할 당시 고등학생이었던 제가 어느새 대학을 졸업하고 직장인이 되었습니다. 당연히 저만 변한 것은 아니고, 함께 대회를 운영하던 친구들도 직장인이나 대학원생이 되면서 PS와의 거리가 멀어졌으며, 대회 운영에 투자할 수 있는 시간도 줄어들었습니다. 이러한 상황에서 한 사람이 모든 책임을 지는 방식은 더 이상 지속 가능하지 않다고 판단했습니다. 따라서 저와 leejseo, ryute가 역할을 분담하기로 했습니다.
후원사(LG전자, 삼성전자 등) 연락은 leejseo가, 스타트링크와의 소통과 예산 관리 ryute가 맡았으며, 저는 행사 기획, 예산안 작성, 각종 플랫폼(드라이브/폴리곤/오버리프) 관리 등 다양한 실무를 담당했습니다. 돌이켜보니 ryute는 제가 제안한 기획안과 예산 편성을 검토하고 최종 승인하는 중요한 역할도 함께 수행했습니다.
이번 대회부터는 Overleaf 서버도 관리해야 했습니다. 2024년 11월부터 Overleaf가 무료 플랜의 프로젝트 공유 인원 한도를 대폭 축소하여 더 이상 대회에서 사용할 수 없게 되었기 때문입니다. 그래서 UCPC 2020 때처럼 self-host Overleaf를 운영하기로 했고, 제가 서버 구축 및 관리를 담당하게 되었습니다.
문제 관리는 의도적으로 맡지 않았습니다. 저는 별다른 어려움 없이 해결할 수 있는 문제(플래티넘 중위권 이하)로만 구성된 대회라면 혼자서도 완벽하게 관리할 자신이 있지만, 그보다 높은 난이도의 문제가 포함되면 퍼포먼스가 급격하게 떨어집니다. 따라서 저보다 실력이 뛰어난 분들을 믿고, 저는 ryute와 함께 중요한 의사결정이 필요할 때만 참여하거나 가끔씩 진행 상황을 확인하는 정도로만 관여했습니다.
행사 기획 - 참가자 선발
대회 준비 초기에 가장 많이 고민했던 부분입니다. 오랜 고민 끝에 다음과 같은 핵심 원칙을 세우고, 이를 충족하면서도 참가자들이 납득할 수 있는 기준을 마련하고자 했습니다.
- 실력이 매우 좋은(수상 후보) 사람이 탈락하지 않아야 함
- BOJ에서 열심히 활동한 사람 우대
- 어뷰징의 가능성이 적어야 함
BOJ 대회의 정체성을 지키고 사칭의 가능성을 배제하기 위해 Codeforces 나 AtCoder 같은 외부 플랫폼은 배제하기로 했습니다. 이 때문에 첫 번째 원칙을 충족하는 기준을 마련하는 것이 특히 어려웠습니다. 논의 과정에서 여러 의견이 나왔고, 최종적으로는 다음과 같이 결정했습니다.
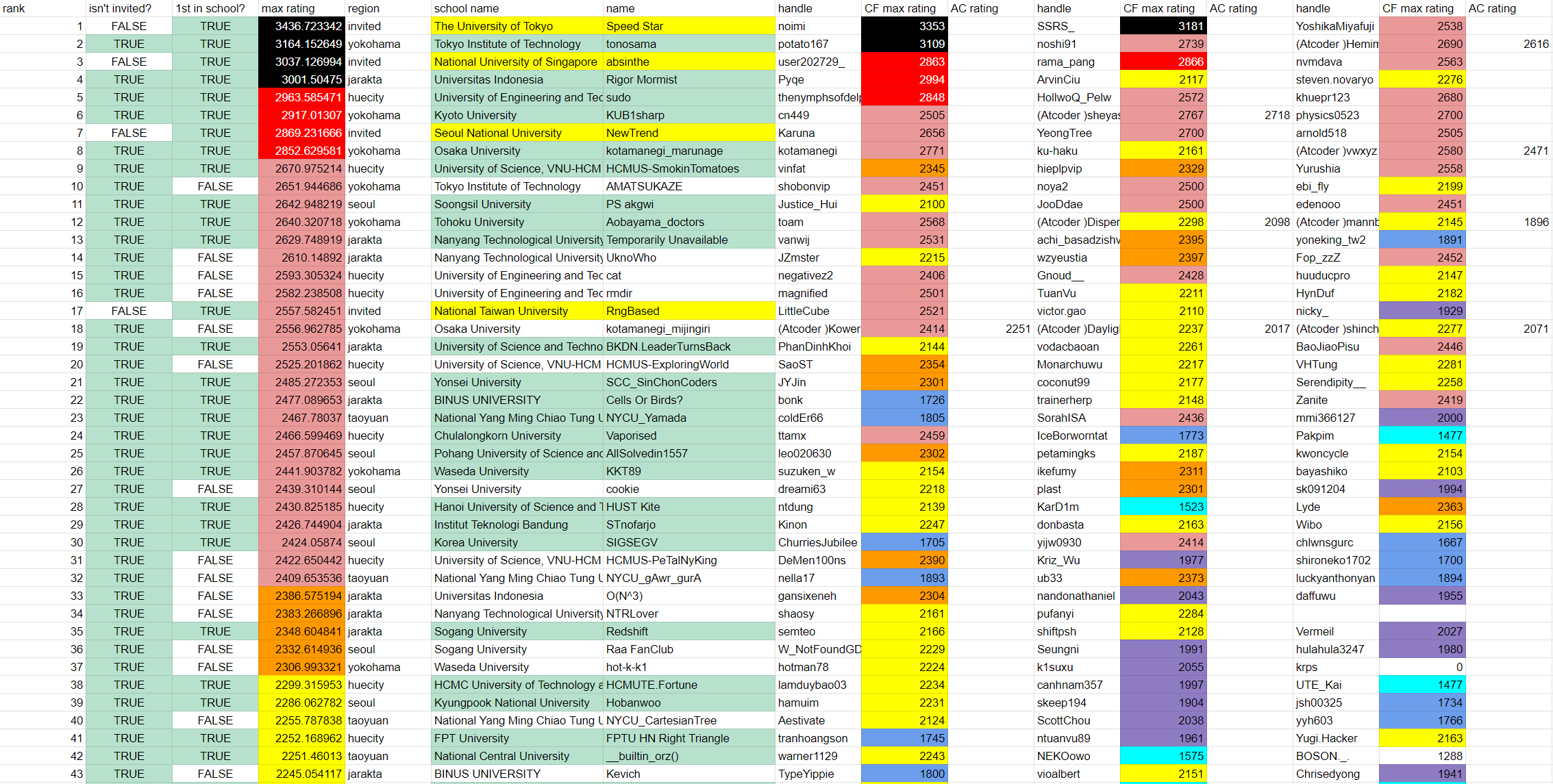
- solved.ac 레이팅 2600(다이아몬드 1) 이상인 사람 중 20명 무작위 추첨, 경쟁률 3.6 : 1
- BOJ에서 난이도가 골드 5 이상인 문제를 500개 이상 해결하고, 총 2000문제 이상 해결한 사람 중 10명 무작위 추첨, 경쟁률 5.6 : 1
- BOJ에서 난이도가 다이아몬드 5 이상인 문제를 가장 많이 해결한 상위 15명, 커트라인 246문제
- BOJ에서 난이도가 플래티넘 5 이상인 문제를 가장 많이 해결한 상위 15명, 커트라인 678문제
- BOJ에서 난이도가 골드 5 이상인 문제를 가장 많이 해결한 상위 12명, 커트라인 1125문제
대회 종료 후 참가자 피드백(31명 응답)은 다음과 같습니다.
| 별점 (평균 4.26) | 1점 | 2점 | 3점 | 4점 | 5점 |
|---|---|---|---|---|---|
| 인원 (총 31명) | 1명 (3.2%) | 0명 (0.0%) | 3명 (9.7%) | 13명 (41.9%) | 14명 (45.2%) |
| D1 이상 | 골드 500/전체 2000문제 | 다이아몬드 top 15 | 플래티넘 top 15 | 골드 top 12 | |
|---|---|---|---|---|---|
| 만족 | 21 | 24 | 19 | 19 | 17 |
| 불만족 | 6 | 5 | 7 | 5 | 4 |
의견 수렴 결과, 1-2번에 비해 3-5번의 만족도가 낮게 나왔습니다. 또한 3-5번의 커트라인이 예산보다 낮았던 점을 고려하면, 향후 유사한 방식으로 참가자를 선정한다면 인원을 줄이는 것도 좋아 보입니다.
행사 기획 - 이벤트
2018년에 논란이 많았던 한 알고리즘 대회에서 주최 측이 “대회가 아닌 축제다”라는 이야기를 했었습니다. 저를 비롯한 알고리즘을 공부하는 사람들은 이 말을 매우 싫어했는데, 대회 자체에 오류도 많았고 진행 과정에서도 잡음이 많았기 때문입니다. 이런 상황에서 “우리는 대회가 아니라 축제를 지향한다”는 말은, 이 분야를 공부하는 사람들뿐만 아니라 분야 자체를 모욕하는 것으로 들렸기 때문입니다.
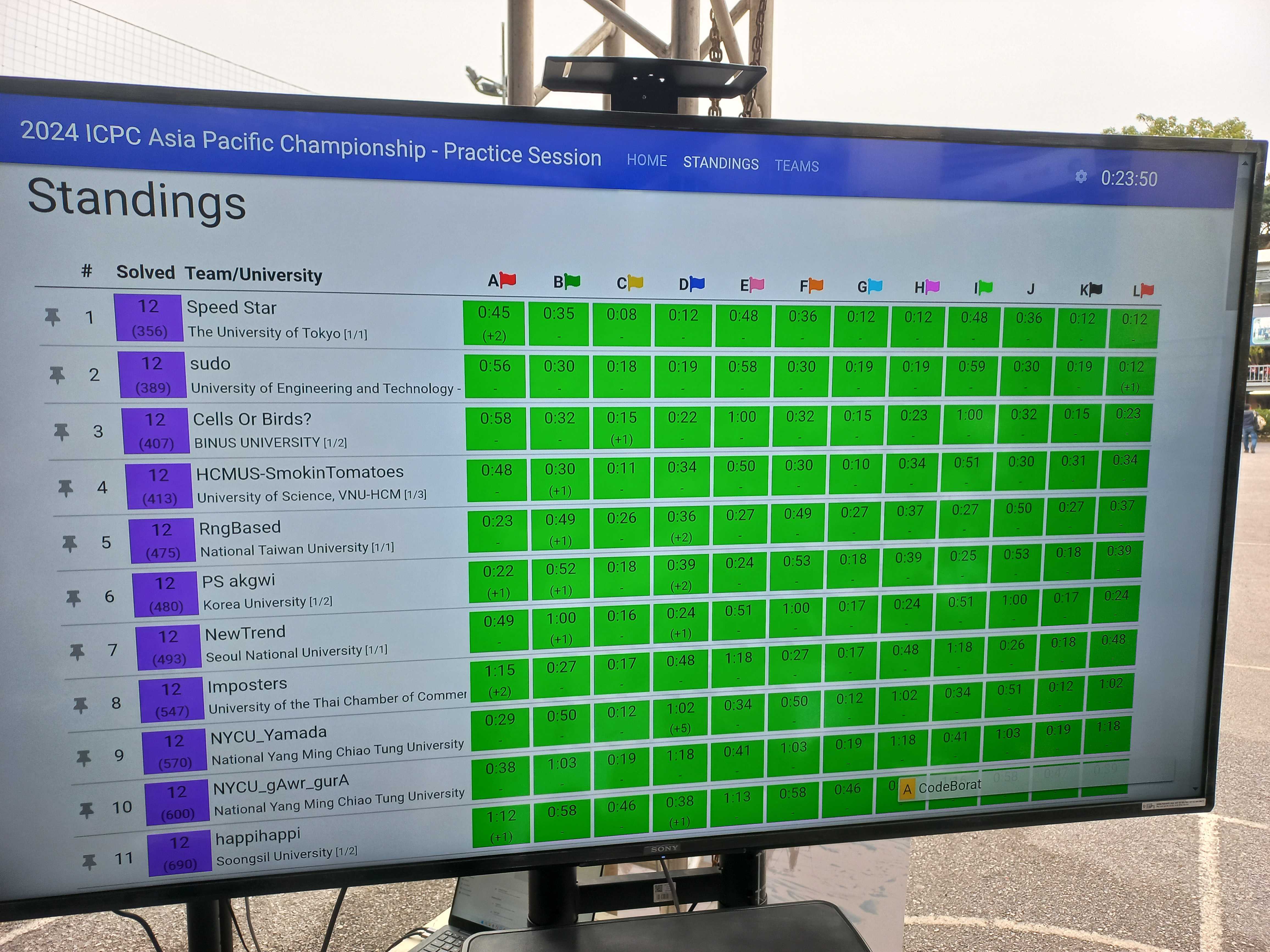
그렇지만 저 역시도 3-5시간 동안 문제만 풀다가 집에 가는 행사보다는, 다양한 재미있는 이벤트를 함께 열어 모두가 즐길 수 있는 행사를 만들어보고 싶다는 생각을 5년 전부터 해왔습니다. 전국에서 알고리즘을 공부하는 사람들이 100명가량 모이는 흔치 않은 기회인 만큼, 하루 종일 함께 즐기다 간다면 더 좋을 테니까요. 예전에 감명 깊게 읽었던 koosaga님의 AtCoder Code Festival 2017 후기(링크)나, 작년에 경험했던 3번의 해외 ICPC 대회(2024 ICPC Asia Pacific Championship, 2023/2024 ICPC World Finals)를 떠올리며, 알고리즘을 열심히 공부한 (대체로 내성적인) 사람들도 충분히 즐길 수 있는 콘텐츠를 기획할 수 있겠다는 확신이 들었습니다.
UCPC와 Hello BOJ 대회는 전통적으로 대회 종료 후 출제자가 각 문제의 풀이를 설명하는 시간을 갖습니다. 하지만 대회가 끝난 뒤 지친 참가자들에게 별로 궁금하지 않을 수도 있는 풀이를 강제로 듣게 하는 것은 고역일 수 있다는 생각을 늘 해왔습니다. 마침 이번에는 출제자가 한 명만 참석했기 때문에 풀이를 진행하지 않을 명분이 생겼고, 이로 따라 생긴 시간을 다른 이벤트로 채우기로 했습니다.
대회 시간을 13:30부터 16:30으로 정한 이유는 여러 가지가 있지만, 가장 중요한 이유는 참가자들에게 식사를 제공할 비용을 줄이기 위해서였습니다. 점심과 저녁 시간 사이 애매한 시간에 대회를 열면 식사 제공을 생략할 수 있기 때문입니다. 대회 앞뒤로 다양한 이벤트를 추가해 식사 시간을 포함하게 되면 대회를 13:00-16:30으로 잡은 이유가 퇴색되기 때문에, 짧은 시간 동안 재미있게 즐길 수 있는 콘텐츠를 준비하기 위해 더욱 신경 썼습니다.
대회 참가자 등록 마감과 시작 사이의 간격이 30분밖에 되지 않고, 대부분의 참가자는 이 시간 동안 오랜만에 만난 사람들과 대화를 나누기 때문에 대회 시작 전 이벤트를 진행하는 것은 어려웠습니다. 따라서 이벤트를 진행할 수 있는 타이밍은 대회 도중과 대회 종료 후뿐입니다. 대회 중에는 더 이상 풀 문제가 없는 참가자를 위해 자리에서 조용히 진행할 수 있는 작은 이벤트를, 대회 종료 후에는 시끌벅적하면서도 내성적인 사람들도 편하게 참여할 수 있는 이벤트를 목표로 준비했습니다.
마침 이번 대회는 로고가 없었고, 준비 기간도 짧아 문제지 표지를 디자인할 시간도 없었습니다. 그래서 문제지 표지 일부를 비워두고, 참가자들이 직접 로고를 그려넣어 응모하는 이벤트를 기획했습니다. BOJ 알파벳을 이용해 캐릭터를 만든 작품, 오토마타를 활용해 ‘Hello BOJ 2025’를 표현한 작품, 체스판과 Knight Tour를 이용해 ‘Hello BOJ 2025’를 구현한 작품 등 흥미로운 결과물이 많이 나왔습니다.
대회 종료 후에는 Kahoot!을 활용한 퀴즈를 진행했습니다. 이는 예전에 친구들과 그림을 보고 어떤 문제인지 맞히는 놀이에서 아이디어를 얻은 것으로, 그림 퀴즈 외에도 BOJ와 PS 분야 전반에 관한 문제를 포함했습니다. 퀴즈 문제와 코멘트는 뒤에서 확인할 수 있습니다.
대회 종료 후 이벤트에 관한 참가자 피드백(31명 응답)은 다음과 같았습니다.
| 별점 | 1점 | 2점 | 3점 | 4점 | 5점 |
|---|---|---|---|---|---|
| 로고 (평균 4.42) | 0명 (0.0%) | 0명 (0.0%) | 3명 (9.7%) | 12명 (38.7%) | 16명 (51.6%) |
| 퀴즈 (평균 5.52) | 0명 (0.0%) | 1명 (3.2%) | 4명 (12.9%) | 4명 (12.9%) | 22명 (71.0%) |
‘대회 중에 로고 이벤트 외에도 조금 더 긴 호흡으로 재미있게 즐길 컨텐츠가 있으면 좋겠다’, ‘PS 과몰입자가 아닌 사람에게는 퀴즈 문제가 어렵다’, ‘대회 직후 풀이를 어떤 형태로든 공개하면 좋을 것 같다’ 라는 의견도 있었습니다.
퀴즈 문제 및 간단한 코멘트
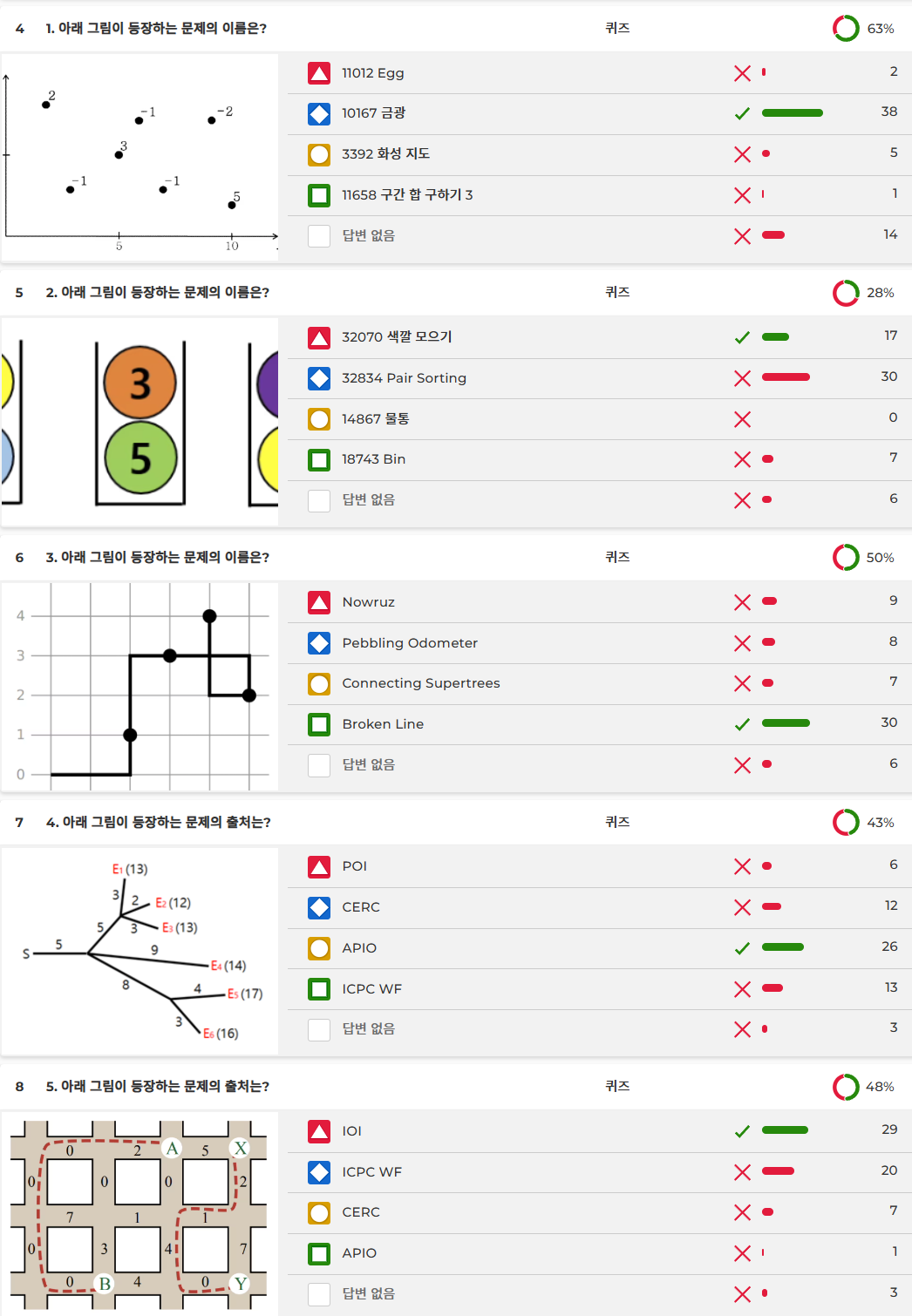
- 1번: 2014 KOI 중등부 4번으로 출제된 ‘금광’ 문제입니다. 2차원 평면 위에서 가중치가 가장 큰 직사각형을 찾는 문제로, 문제의 선지는 2차원 쿼리 문제들로 채웠습니다.
- 2번: 2024 KOI 중등부 2번으로 출제된 ‘색깔 모으기’ 문제입니다. 문제의 선지로는 같은 소재로 2024 ICPC Seoul Regional Contest에 출제된 ‘Pair Sorting’ 문제, 그리고 그림을 보고 떠오르는 키워드인 물통(2017 KOI 고등부 1번)과 Bin(Tourist Contest 5)을 넣었습니다. 2024 서울 리저널에 출제된 ‘Pair Sorting’ 문제에 낚인 대학생들이 많았습니다.
- 3번: IOI 2019에 출제된 output only 문제 ‘Broken Line’입니다. 문제의 선지로는 각각 2017년과 2012년에 출제된 output only 문제인 ‘Nowruz’와 ‘Pebbling Odometer’, 그리고 IOI 2020에 출제된 ‘Connecting Supertrees’를 넣었습니다.
- 4번: APIO 2016에 출제된 ‘Fireworks’입니다. 문제 그림이 POI 스타일이라서 POI와 폴란드 소속 대학이 참가하는 CERC를 문제 선지에 넣었습니다.
- 5번: IOI 2013에 출제된 ‘Wombats’입니다. 문제 선지는 별생각 없이 채웠습니다.
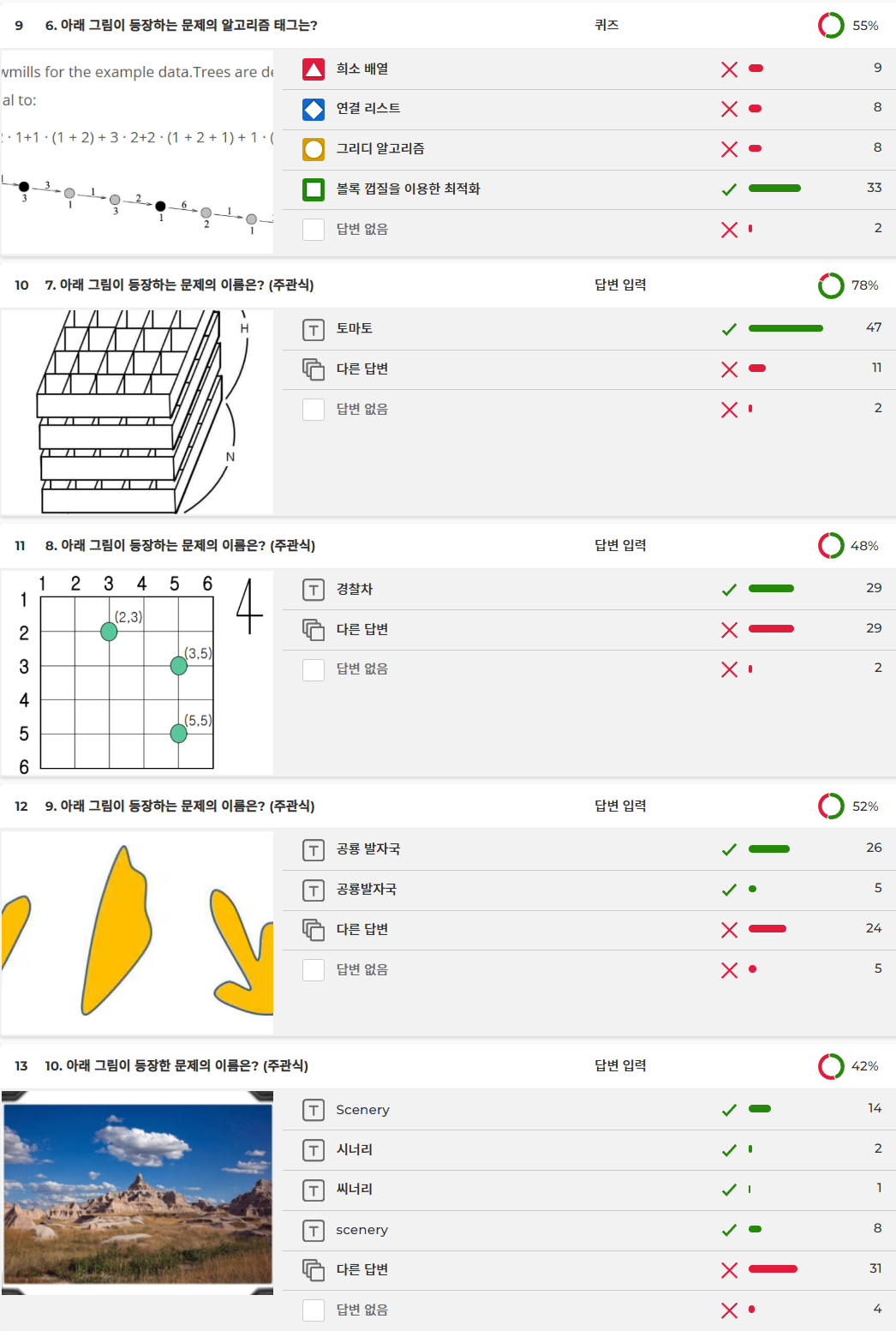
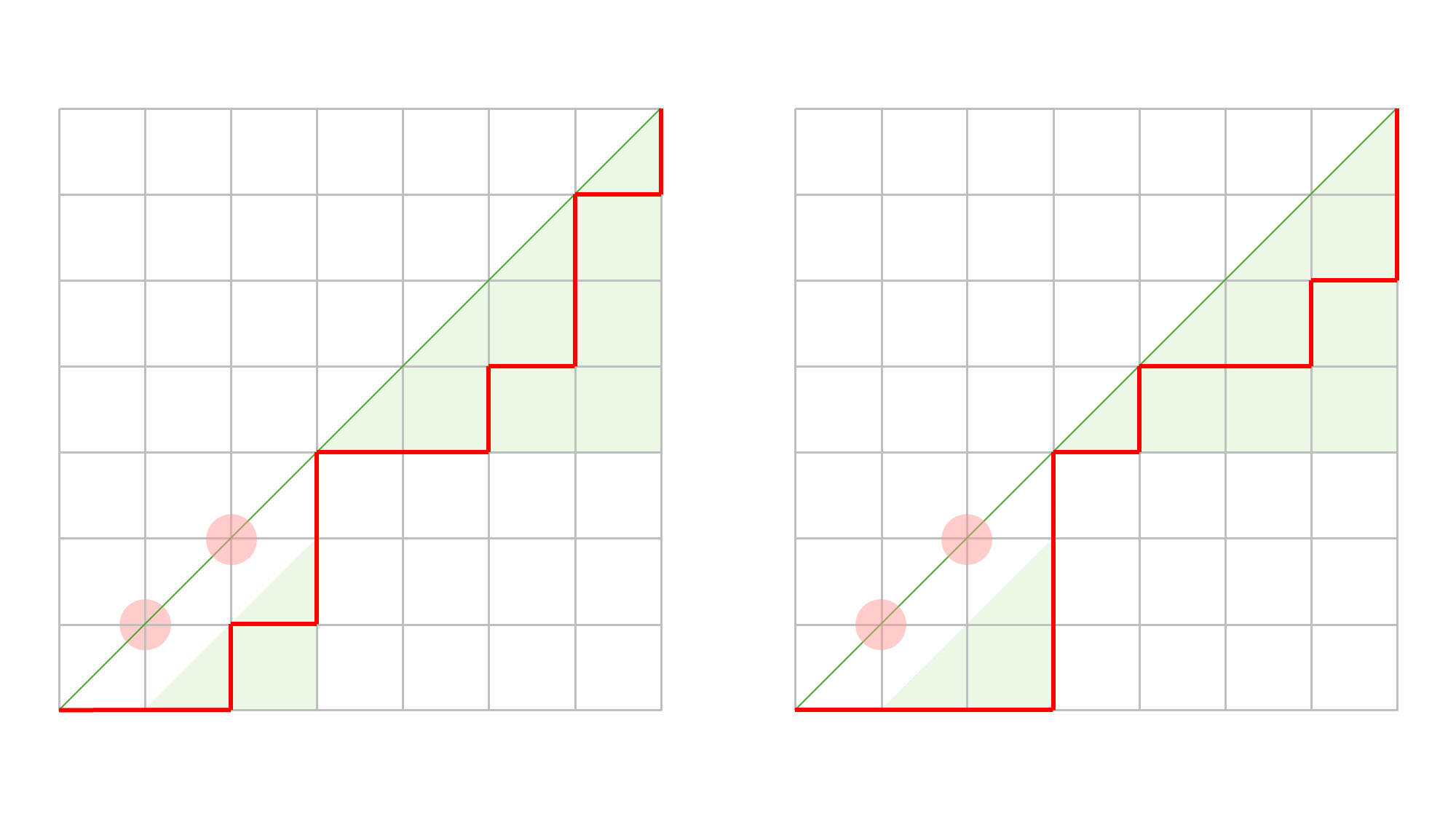
- 6번: CEOI 2004에 출제된 ‘Two sawmills’에서 가져왔습니다. 식이 APIO 2010의 ‘Commando’(특공대)처럼 생겼다는 것을 파악하면 Convex Hull Trick 문제라는 것을 어렵지 않게 파악할 수 있습니다. 문제 선지는 여러 LLM 모델에게 퀴즈를 낸 뒤 생성된 답안으로 채웠습니다.
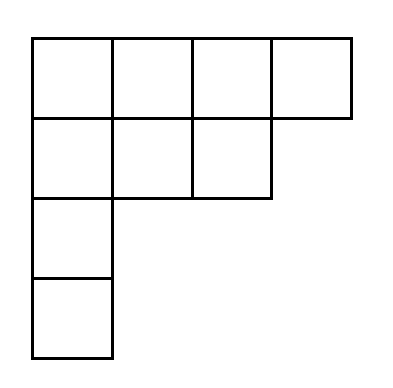
- 7번: 2013 KOI 지역 본선 초등부 3번으로 출제된 ‘토마토’ 문제입니다. 원래는 초등부 3번 토마토(3차원)와 고등부 1번 토마토(2차원) 중에서 맞추는 것을 출제하려고 했지만, 너무 어려워서 수정했습니다.
- 8번: 2003 KOI 중등부 2번으로 출제된 ‘경찰차’ 문제입니다.
- 9번: 2018 KOI 중등부 4번으로 출제된 ‘공룡 발자국’ 문제입니다.
- 10번: 2017 ICPC World Finals에 출제된 ‘Scenery’ 문제입니다.
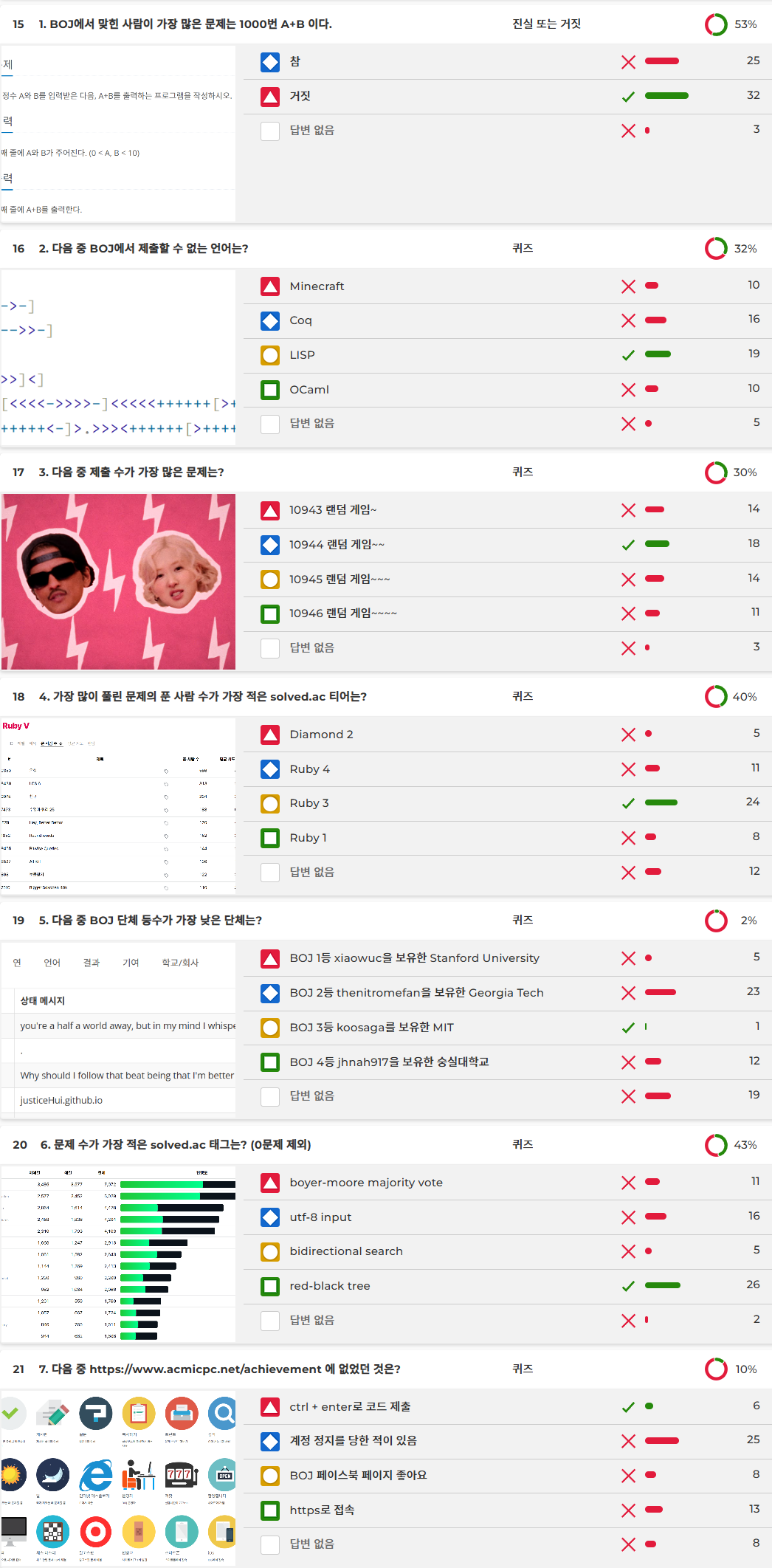
- 1번: 가장 많이 풀린 문제는 BOJ 2557. Hello World 입니다.
- 2번: Minecraft와 Coq을 사용하는 문제는 2020년 구데기컵에 출제되었습니다.
- 3번: AC 확률이 1/10000 인 10944. 랜덤 게임~~ 문제가 가장 제출이 많습니다.
- 4번: 티어별로 가장 많이 풀린 문제는 다음과 같습니다.
- D2: BOJ 13324. BOJ 수열 2, 468명
- D1: BOJ 17474. 수열과 쿼리 26, 476명
- R5: BOJ 10350. 은행, 589명
- R4: BOJ 18440. LCS 7, 167명
- R3: BOJ 18789. 814 - 2, 78명
- R2: BOJ 14640. Scenery, 109명
- R1: BOJ 18236. 행렬 곱셈 순서 2, 89명
- 5번: Georgia Tech > 숭실대학교 > Stanford > MIT 순입니다.
- 6번: red-black tree 태그가 달린 문제는 1문제뿐입니다.
- 7번: achievement 페이지에 ctrl + enter 으로 코드 제출은 없었습니다.
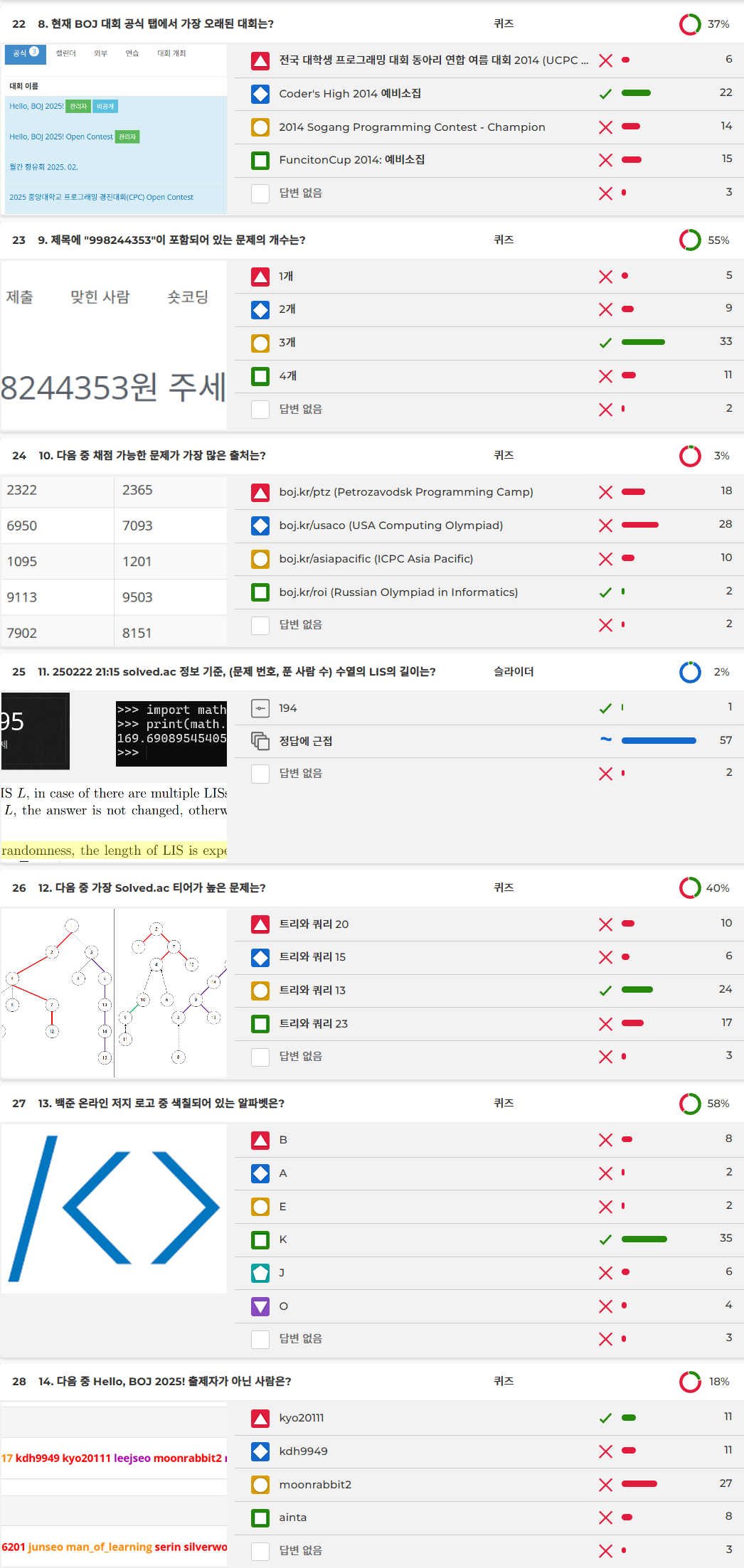
- 8번: UCPC 2014 예선과 합수컵 2014 예비 소집은 존재하지 않는 대회입니다.
- 9번: 이미지에서 보이는 문제와 NPM998244353 Easy/Hard까지 총 3문제입니다.
- 10번: ROI 밑에 있는 Internet Olympiads in Informatics 에 문제가 매우 많습니다. 문제 선지로는 일부러 대회가 여러 번 열리는 USACO와 Ptz Camp를 넣었습니다.
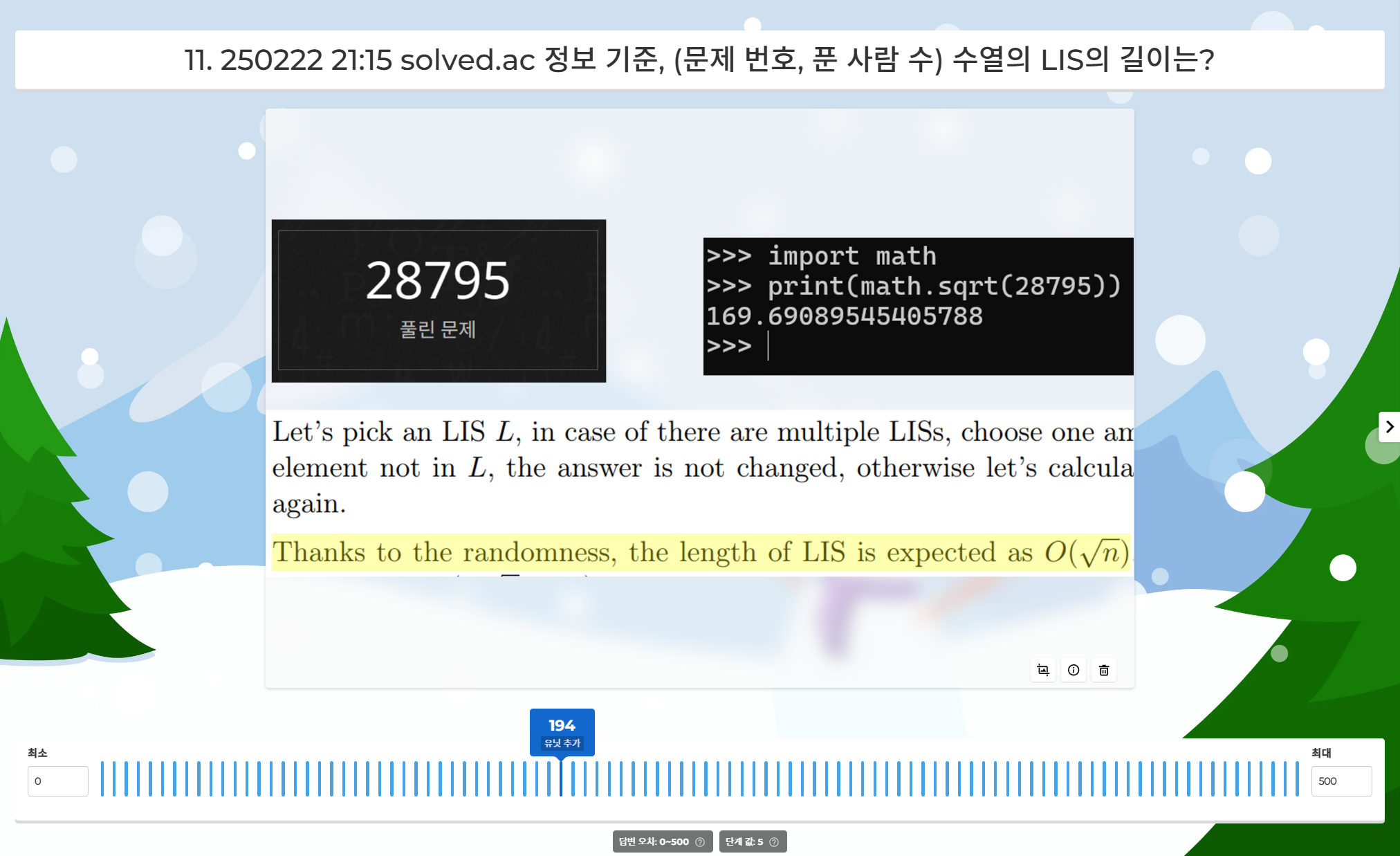
- 11번: 길이가 $n$인 순열의 LIS 길이의 기댓값은 약 $2 \sqrt n$입니다. $\sqrt n$과 $2\sqrt n$ 사이에서 적당히 찍으면 괜찮은 점수를 받을 수 있습니다.
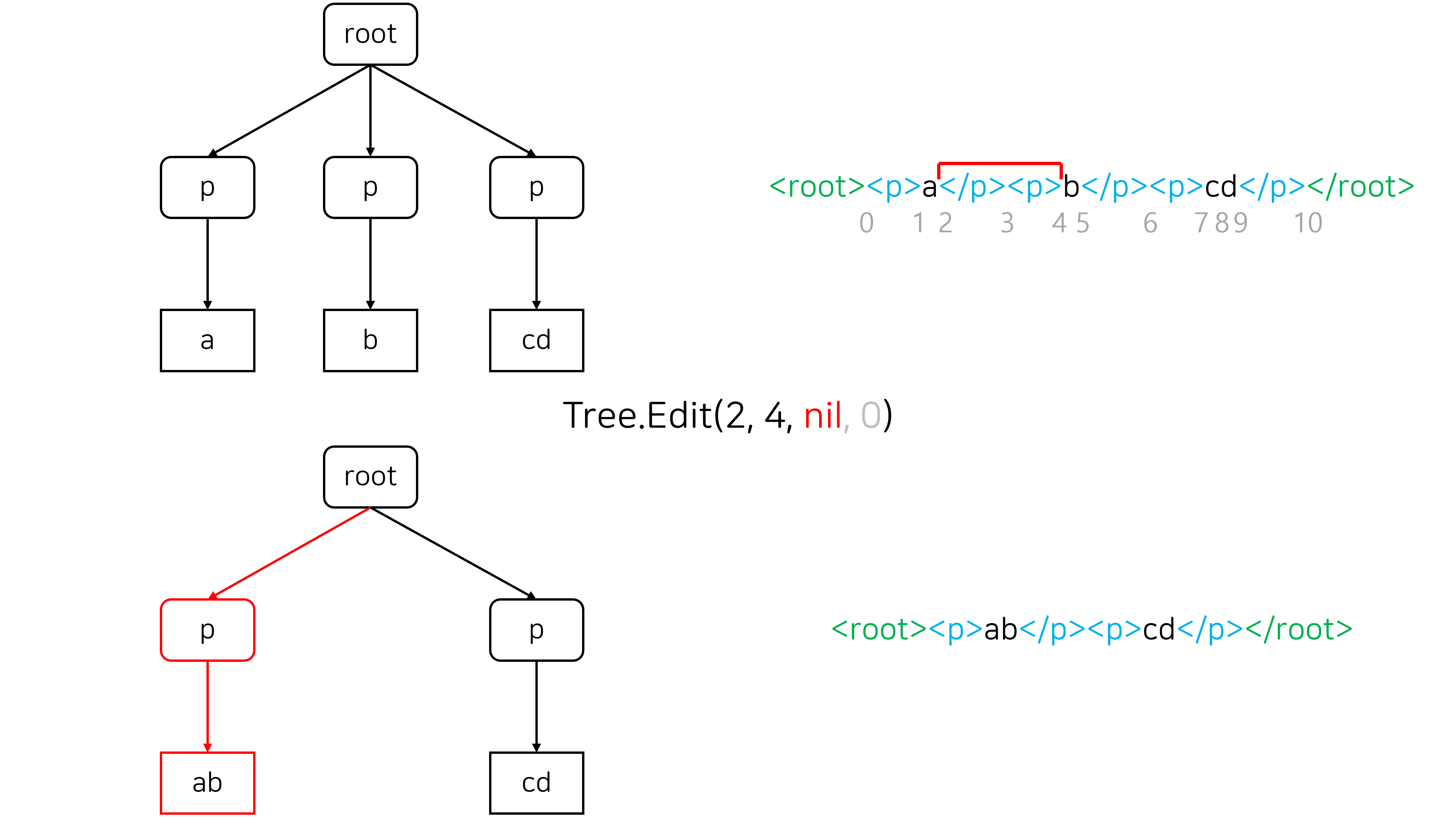
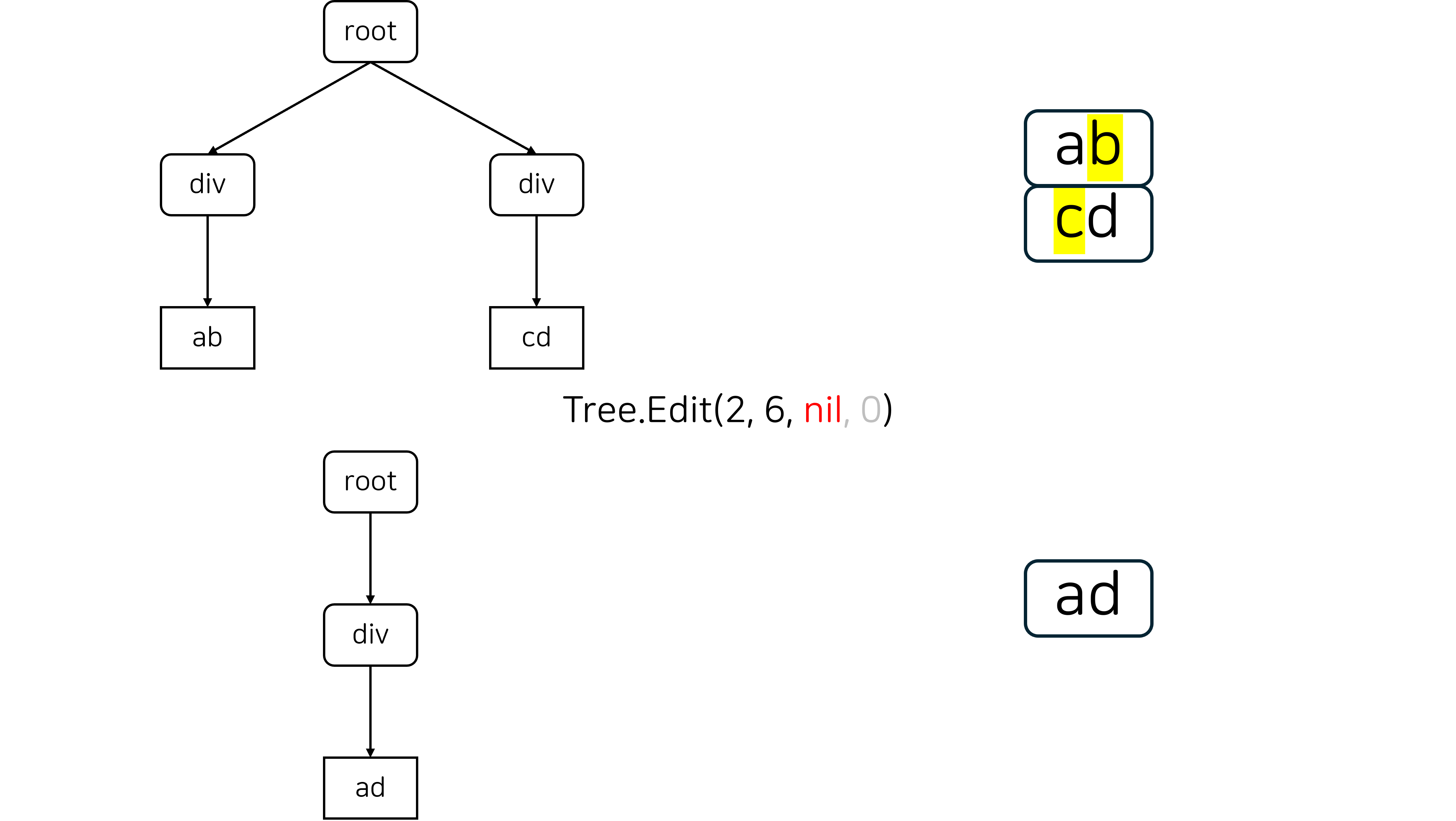
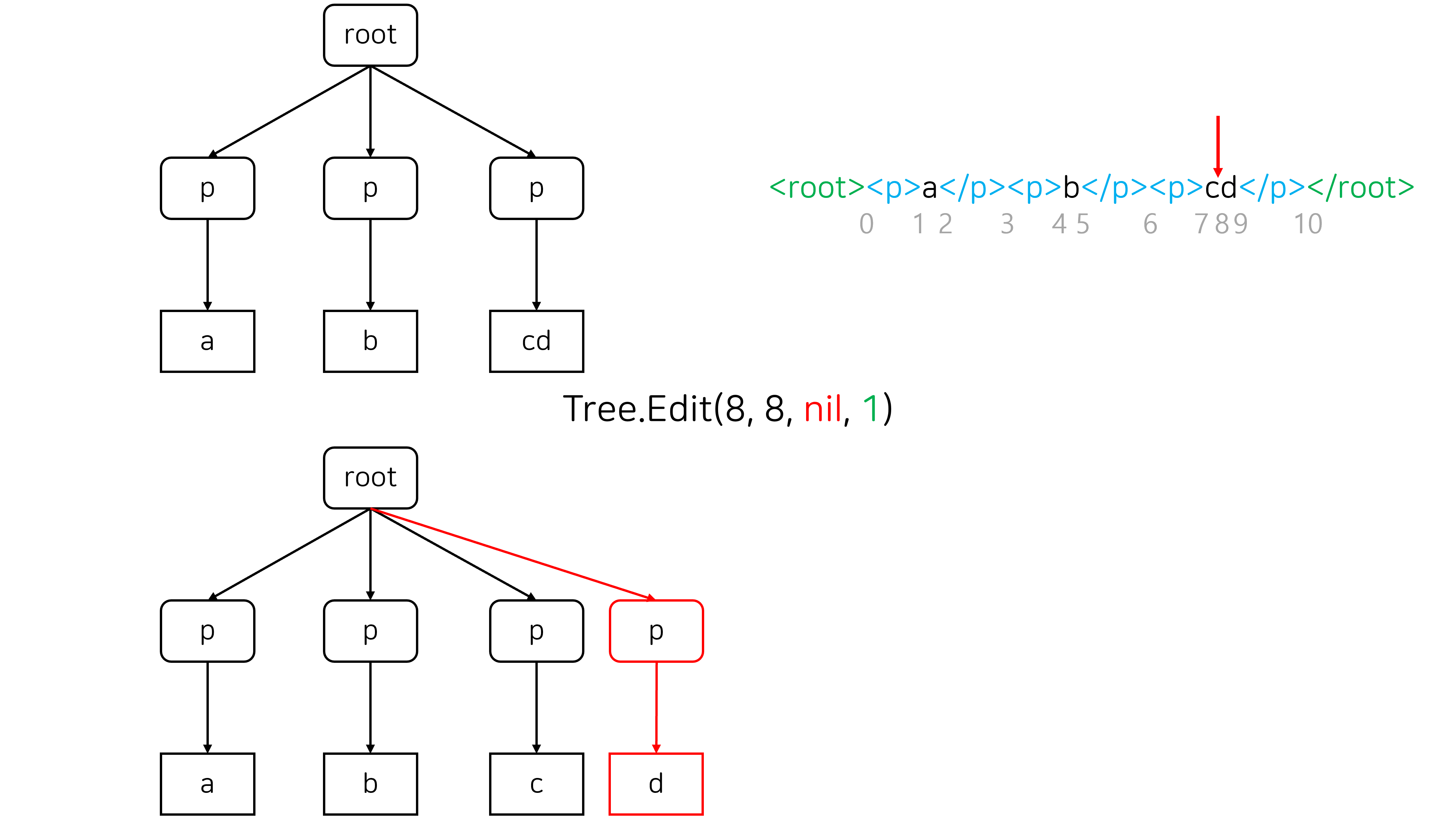
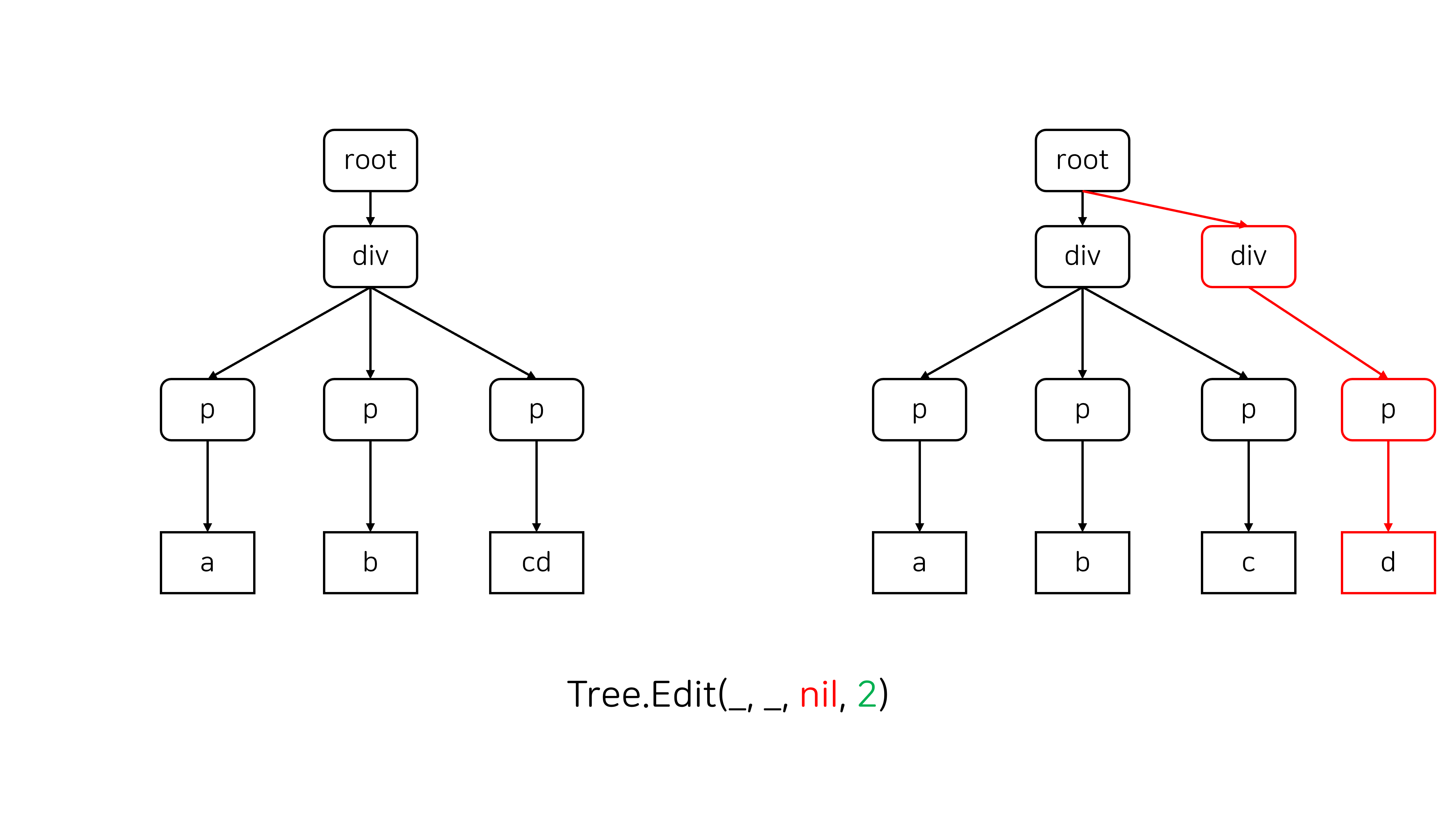
- 12번: 트리와 쿼리 13은 경로 쿼리와 서브트리 쿼리를 포함해 총 12개의 쿼리가 주어지는 루비 1 문제입니다.
- 13번: 그림을 잘 봅시다.
- 14번: kdh9949님은 ABCF번, moonrabbit2님은 G번, ainta님은 D번을 출제하셨습니다. kyo20111님과 kdh9949님은 Goodbye와 Hello 대회에 자주 출제하셨기 때문에, ainta님도 cki86201님처럼 모든 문제를 검수하는 역할로 생각하도록 유도하기 위해 선지를 구성했는데, 의도한 대로 되지 않았습니다. 많은 사람들이 G번 문제를 읽을 시간이 없었던 것이 큰 영향을 미친 것 같습니다.
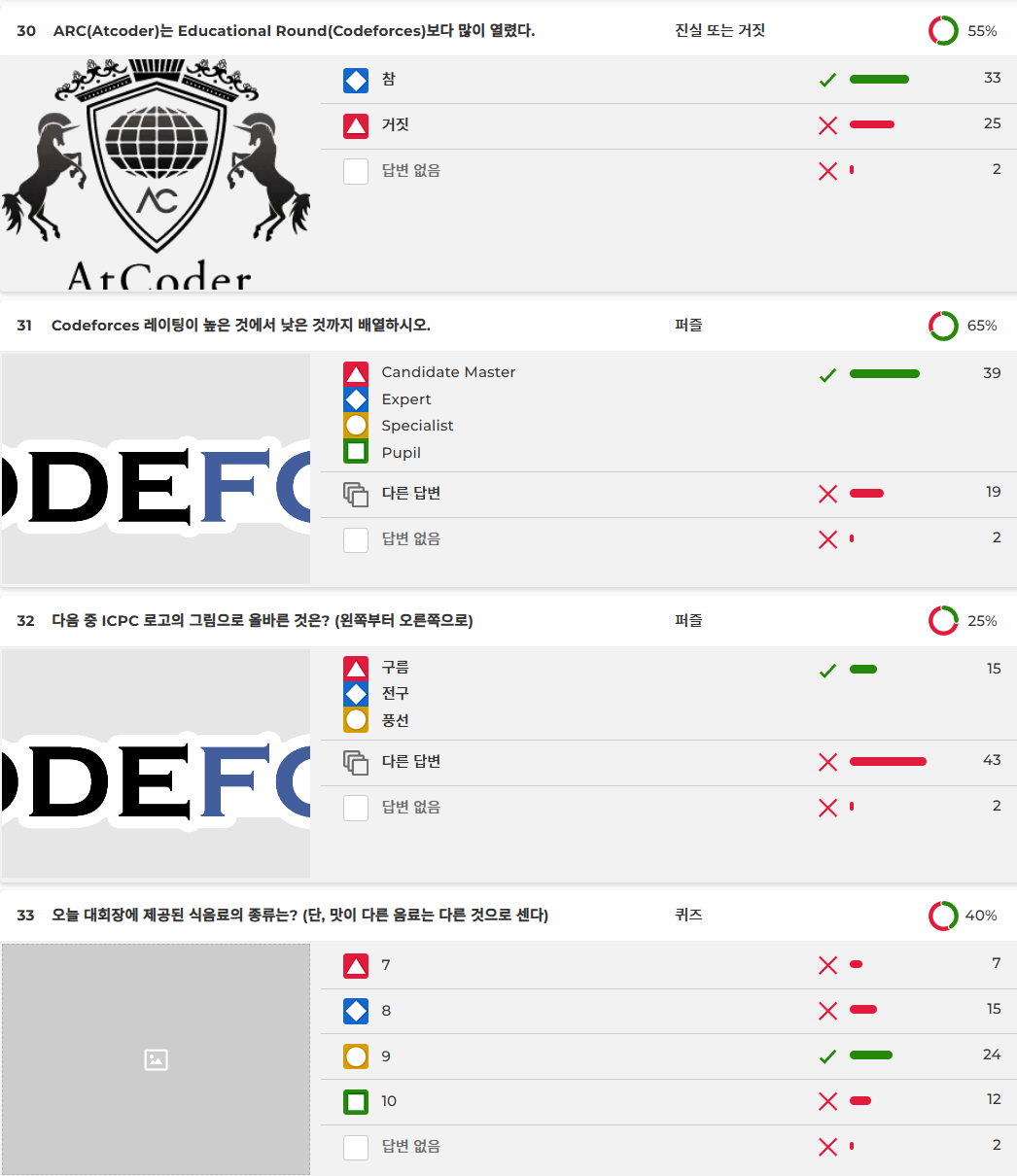
원래는 첫 번째 문제에서 ICPC 로고를 보여준 다음, 두 번째 문제에서 Codeforces 로고를 보여주면서 ICPC 색깔 순서를 물어보고, 세 번째 문제에서 AtCoder 로고를 보여주면서 Codeforces 색깔 순서를 물어보려고 했었습니다. 욕 많이 먹을 것 같아서 실천하지는 않았습니다.
마무리
다행히 올해도 큰 문제 없이 성공적으로 대회를 마무리 지었습니다. 매번 하는 이야기지만, 2019년과 2020년에 친구들과 별생각 없이 열었던 대회가 너무 커져 버려서 2021년부터 매년 작지 않은 부담을 느끼며 대회를 준비하고 있습니다. 빅뱅의 지드래곤이 무대를 준비하면서 했던 말처럼, ‘잘해도 본전’이라는 말이 딱 어울리는 것 같습니다. 다행히 한 번도 빠지지 않고 매년 대회를 같이 준비하는 ryute와 leejseo, 그리고 대회 운영과 문제 작업을 담당해 주시는 많은 분들 덕분에 항상 멋진 대회를 개최하고 있습니다. 정말 감사합니다. 대회를 후원해 주신 스타트링크, 솔브드, 삼성전자 소프트웨어멤버십, LG전자에도 이 자리를 빌려 감사의 말씀을 전합니다.
이 대회를 계속 운영할지, 아니면 놓아줄지는 항상 고민하는 주제입니다. 작년 3월에 두 번째 ICPC World Finals 진출을 확정 지은 이후로 PS와 점점 멀어지고 있으며, 직장에 들어오고 대학을 졸업한 이후로는 더 빠른 속도로 멀어지고 있습니다. 아마 예전(2019-2023년)처럼 열정적으로 PS를 연습할 일은 영원히 없지 않을까 싶습니다. 글을 올려다 보니 문제 이야기가 하나도 없는 게 PS와 멀어지고 있는 게 실감이 나네요.
그럼에도 불구하고 PS는 정말 좋은 취미이며, 친구들과 대회를 열고 참가자들이 즐거워하는 모습을 보는 것은 제가 가장 큰 보람을 느끼는 일 중 하나입니다. 앞으로 반년 동안 잘 고민하고 올해 9월에 결정하려고 합니다. 그런데 아마 하지 않을까요? 잘 모르겠습니다.
대회에 참가해 주신 분들과 길고 재미없는 이 글을 끝까지 읽어주신 분들께 감사드립니다.
]]>