선린정보올림피아드 풀이 및 후기

작성일 | In

서론

9월 1일에 진행한 선린정보올림피아드(선린 정보 알고리즘 경시대회) 문제 풀이와 후기입니다.
6문제 150분 셋이고, 문제가 오늘 BOJ에 올라갔기 때문에 지금 풀이를 작성합니다.

문제 난이도는 solved.ac 기준으로 브론즈, 실버, 골드 중상위권, 골드 상위권, 플래티넘 중위권, 플래티넘 상위권~다이아 하위권으로 생각하고 있습니다.

결과


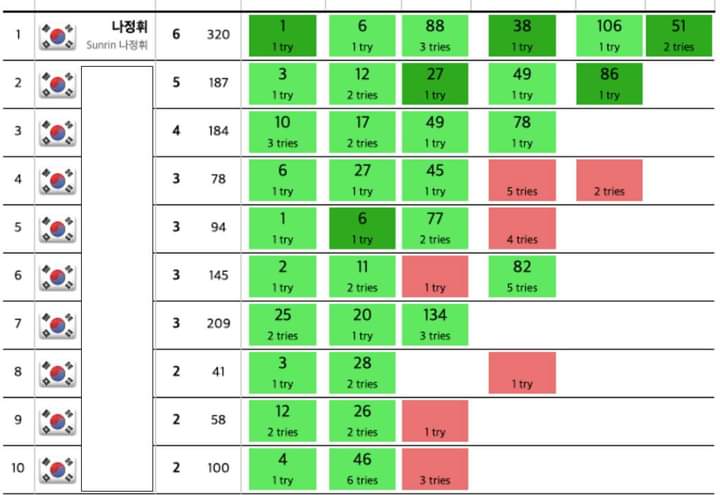
1등했습니다.

  • 29명 참가
  • 6문제 1명 (ABCDEF)
  • 5문제 1명 (ABCDE)
  • 4문제 1명 (ABCD)
  • 3문제 4명 (ABC 3명, ABD 1명)
  • 2문제 9명 (AB)
  • 1문제 10명 (A)
  • 0문제 3명
  • A 26명 / B 1명 / C 6명 / D 4명 / E 2명 / F 1명

대회 후기는 문제 풀이 밑에 적었습니다.

A. 헛간 청약

문제 링크

$\min(N, \lfloor \frac{W}{L} \rfloor \times \lfloor \frac{H}{L} \rfloor)$

1
2
3
4
5
6
7
8
#include <bits/stdc++.h>
using namespace std;

int main(){
    ios_base::sync_with_stdio(false); cin.tie(nullptr);
    int n, w, h, l; cin >> n >> w >> h >> l;
    cout << min(n, (w/l) * (h/l));
}

B. 소-난다!

문제 링크

에라토스테네스의 체로 전처리해두면 소수 판별은 $O(1)$에 할 수 있습니다.
$M$개의 원소를 선택하는 조합들은 비트마스킹을 이용해 완전 탐색을 해주면 $O(2^N \times N)$에 모두 볼 수 있습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;

bool isp[10101];
void sieve(){
    memset(isp, 1, sizeof isp); isp[0] = isp[1] = 0;
    for(int i=2; i<10101; i++) if(isp[i]) {
        for(int j=i+i; j<10101; j+=i) isp[j] = 0;
    }
}
int n, m, a[11]; set<int> st;
int main(){
    ios_base::sync_with_stdio(false); cin.tie(nullptr);
    cin >> n >> m; for(int i=0; i<n; i++) cin >> a[i]; sieve();
    for(int bit=0; bit<(1<<n); bit++){
        int sum = 0, cnt = 0;
        for(int i=0; i<n; i++) if(bit & (1 << i)) cnt++, sum += a[i];
        if(cnt == m && isp[sum]) st.insert(sum);
    }
    if(st.empty()){ cout << -1; return 0; }
    for(auto i : st) cout << i << " ";
}

C. 수업

문제 링크

키가 큰 수강생부터 차례대로 보면서, 크기가 $k$ 미만인 집합 중 가장 큰 집합에 넣어주는 그리디가 성립한다는 것은 쉽게 알 수 있습니다.
이를 $O(N^2)$보다 빠르게 구현하는 것이 힘들 수 있는데, 저는 Fenwick Tree와 Parametric Search를 이용해 $O(N \log^2 N)$에 구현했습니다. 자세한 구현은 아래 코드를 참고하시면 됩니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;

typedef long long ll;
typedef pair<ll, ll> p;

int tree[505050];
void update(int x, int v){
    for(x++; x<505050; x+=x&-x) tree[x] += v;
}
int query(int x){
    int ret = 0;
    for(x++; x; x-=x&-x) ret += tree[x];
    return ret;
}
int query(int l, int r){ return query(r) - query(l-1); }

int n; p inp[505050], ans; vector<int> v;

int main(){
    ios_base::sync_with_stdio(false); cin.tie(nullptr);
    cin >> n; for(int i=1; i<=n; i++) cin >> inp[i].x >> inp[i].y;
    sort(inp+1, inp+n+1, greater<>());
    for(int i=1; i<=n; i++) v.push_back(inp[i].y);

    for(auto i : v){
        int l = 1, r = i-1;
        if(!query(r)){ ans++; update(1, 1); continue; }
        while(l < r){
            ll m = l + r + 1 >> 1;
            if(query(m, r)) l = m;
            else r = m - 1;
        }
        update(l, -1); update(l+1, 1);
    }
    cout << ans;
}

D. 소 운전한다.

문제 링크

각 정점을 (1)돈까스를 먹은 상태와 (2)돈까스를 먹지 않은 상태로 분할해줍시다. 돈까스를 먹지 않은 상태로 $v$에 도착한 상태를 $v_0$, 먹은 상태로 $v$에 도착한 상태를 $v_1$로 정의합시다.

그래프를 구성하는 것은 아래와 같이 하면 됩니다.
모든 고속도로 $(x, y, t, k)$에 대해

  • $x_0$에서 $y_0$으로 가는 가중치 $t$ 간선 생성
  • $y_0$에서 $x_0$으로 가는 가중치 $t$ 간선 생성
  • $x_1$에서 $y_1$으로 가는 가중치 $t$ 간선 생성
  • $y_1$에서 $x_1$으로 가는 가중치 $t$ 간선 생성
  • $x_0$에서 $y_1$으로 가는 가중치 $t-k$ 간선 생성
  • $y_0$에서 $x_1$으로 가는 가중치 $t-k$ 간선 생성

$t-k$가 음수가 될 수 있기 때문에 다익스트라 알고리즘을 돌리기 꺼려집니다.
가중치가 $t-k$ 꼴인 간선은 정확히 한 번만 지나기 때문에, 해당 가중치에 $10^{18}$을 더해준 상태로 다익스트라 알고리즘을 돌린 뒤 최종 결과에서 $10^{18}$을 빼주면 됩니다.

대회 도중에는 시간 제한이 넉넉하고 데이터가 약해서 SPFA를 이용해 $O(V+E)$같은 $O(VE)$로 풀 수 있었지만, BOJ에서는 다익스트라를 이용해 $O(E \log V)$에 풀어야 합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;

typedef long long ll;
typedef pair<ll, ll> p;
const ll inf = 1e18;

int n, m;
vector<p> g[202020];
ll dst[202020];

int main(){
    ios_base::sync_with_stdio(false); cin.tie(nullptr);
    cin >> n >> m;
    for(int i=1; i<=m; i++){
        ll s, e, x, y; cin >> s >> e >> x >> y;
        g[s << 1].emplace_back(e << 1, x);
        g[e << 1].emplace_back(s << 1, x);
        g[s << 1 | 1].emplace_back(e << 1 | 1, x);
        g[e << 1 | 1].emplace_back(s << 1 | 1, x);
        g[s << 1].emplace_back(e << 1 | 1, inf+x-y);
        g[e << 1].emplace_back(s << 1 | 1, inf+x-y);
    }

    memset(dst, 0x3f, sizeof dst);
    priority_queue<p> pq; pq.emplace(0, 2); dst[2] = 0;
    while(pq.size()){
        ll now = pq.top().y, cst = -pq.top().x; pq.pop();
        if(cst > dst[now]) continue;
        for(auto i : g[now]){
            if(dst[i.x] > cst + i.y){
                dst[i.x] = cst + i.y;
                pq.emplace(-dst[i.x], i.x);
            }
        }
    }
    for(int i=2; i<=n; i++) cout << dst[i << 1 | 1]-inf << "\n";
}

E. 친구

문제 링크

모든 정점의 차수가 $\frac{N}{2}$ 이상인 그래프에서 해밀턴 사이클을 찾는 문제입니다.

인접하지 않은 두 정점 $u, v$에 대해 $degree(u) + degree(v) \geq N$이 성립하므로, Ore’s Theorem과 Palmer’s Algorithm를 사용해서 $O(N^2)$만에 문제를 풀 수 있습니다. 자세한 설명은 위 링크를 참고하시기 바랍니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>
#define x first
#define y second
#define all(v) v.begin(), v.end()
#define compress(v) sort(all(v)), v.erase(unique(all(v)), v.end())
using namespace std;

typedef long long ll;
typedef pair<int, int> p;

int n, w[111][111], ans[111];
vector<int> g[111];

int main(){
    ios_base::sync_with_stdio(false); cin.tie(nullptr);
    cin >> n;
    for(int i=1; i<=n; i++) for(int j=1; j<=n; j++){
        cin >> w[i][j];
        if(w[i][j]) g[i].push_back(j);
    }
    for(int i=1; i<=n; i++) ans[i] = i;
    while(1){
        int flag = 1, idx;
        for(int i=1; i<=n; i++){
            int j = i + 1; if(i == n) j = 1;
            if(!w[ans[i]][ans[j]]){ flag = 0; idx = i; break; }
        }
        if(flag) break;
        for(int j=1; j<=n; j++){
            int i = idx;
            int ii = i + 1, jj = j + 1;
            if(i == n) ii = 1;
            if(j == n) jj = 1;
            if(w[ans[i]][ans[j]] && w[ans[ii]][ans[jj]]){
                if(i < j) swap(ans[ii], ans[j]);
                else swap(ans[jj], ans[i]);
                break;
            }
        }
    }
    for(int i=1; i<=n; i++) cout << ans[i] << " ";
}

F. 실험

문제 링크

2-SAT의 느낌이 강하게 오는 것 같으니, 식을 세워봅시다.

조건 2는 $(i ∨ j)$이고, $￢i ⇒ j, \space ￢j ⇒ i$로 나타낼 수 있습니다.

조건 1은 $A_1, A_2, \ldots , A_k$ 중 최대 1개를 선택하는 것인데, Naive하게는 $(￢i ∨ ￢j)$ 꼴의 CNF $O(k^2)$개로 나타낼 수 있습니다. 하지만 $k \leq 500\,000$이기 때문에 최적화를 해야합니다. $O(k)$개의 CNF로 나타낼 수 있습니다.

$B_1, B_2, \ldots , B_k$라는 총 $k$개의 새로운 변수를 만들고, $B_i$는 $A_1 ∨ A_2 ∨ \ldots ∨ A_i$와 동치가 되도록 만듭시다. 아래 조건을 넣어주면 됩니다.

  1. $B_i ⇒ B_{i+1}$
  2. $A_i ⇒ B_i$
  3. $B_i ⇒ ￢A_{i+1}$

1, 2번 조건은 $B_i$와 $A_1 ∨ A_2 ∨ \ldots ∨ A_i$가 동치가 되도록 만들기 위해 필요합니다.
3번 조건은 $i < j$일 때 $(￢i ∨ ￢j)$가 되도록 만드는데 필요합니다.

이렇게 만든 그래프 위에서 2-SAT을 돌려주면 됩니다.

간선 개수이 많아서 BOJ에서는 시간 제한이 빡빡합니다. 코사라주 대신 타잔 알고리즘을 돌리는 것이 정신 건강에 이롭습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#pragma GCC optimize ("O3")
#include <bits/stdc++.h>
#define x first
#define y second
#define all(v) v.begin(), v.end()
#define compress(v) sort(all(v)), v.erase(unique(all(v)), v.end())
using namespace std;

int n, m, a, b, pv = 1;
vector<int> group[101010];
vector<int> g[1212121];
const int inv = 600000;

int up[1212121], vst[1212121], chk[1212121];
vector<int> stk;

inline void addEdge(int s, int e){ g[s].push_back(e); }

int cnt;
void dfs(int v){
    up[v] = vst[v] = ++cnt; stk.push_back(v);
    for(auto i : g[v]){
        if(!vst[i]) dfs(i), up[v] = min(up[v], up[i]);
        else if(!chk[i]) up[v] = min(up[v], vst[i]);
    }
    if(up[v] == vst[v]){
        cnt++;
        while(stk.size()){
            int t = stk.back(); stk.pop_back();
            chk[t] = cnt; if(t == v) break;
        }
    }
}

int getSCC(){
    for(int i=1; i<=n; i++){
        if(!vst[i]) dfs(i);
        if(!vst[i+inv]) dfs(i+inv);
    }
    for(int i=1; i<pv; i++){
        if(!vst[i+n]) dfs(i+n);
        if(!vst[i+n+inv]) dfs(i+n+inv);
    }
    for(int i=1; i<=n; i++) if(chk[i] == chk[i+inv]) return 0;
    for(int i=1; i<pv; i++) if(chk[i+n] == chk[i+n+inv]) return 0;
    return 1;
}

int main(){
    ios_base::sync_with_stdio(false); cin.tie(nullptr);
    cin >> n >> m >> a >> b;
    for(int i=1; i<=a; i++){
        int uid, gid; cin >> uid >> gid;
        group[gid].push_back(uid);
    }
    for(int i=1; i<=b; i++){
        int x, y; cin >> x >> y;
        addEdge(x+inv, y); addEdge(y+inv, x);
    }
    for(int i=1; i<=m; i++){
        if(group[i].empty()) continue;
        for(int j=0; j<group[i].size(); j++){
            // A_i => B_i
            addEdge(group[i][j], n+pv+j);
            addEdge(n+pv+j+inv, group[i][j]+inv);
            if(j){
                // B_{i-1} => B_i
                addEdge(n+pv+j-1, n+pv+j);
                addEdge(n+pv+j+inv, n+pv+j-1+inv);
                // B_{i-1} => ~A_i
                addEdge(n+pv+j-1, group[i][j]+inv);
                addEdge(group[i][j], n+pv+j-1+inv);
            }
        }
        pv += group[i].size();
    }
    if(getSCC()) cout << "TAK";
    else cout << "NIE";
}

대회 후기

  • (00:00 - 00:06) A, B는 매우 쉬운 문제로 6분동안 두 문제를 빠르게 밀고 시작했습니다.
  • (00:06 - 00:2x) C를 읽고 그리디 풀이가 생각났지만 증명을 못했고, 조금 더 고민하면 말릴 것 같아서 D로 넘어갔습니다.
  • (00:2x - 00:38) 음수 가중치가 있는 최단경로 문제입니다. 조금 더 생각하면 다익스트라 알고리즘을 이용해 $O(E \log V)$에 풀 수 있었지만, 대회 중에는 그럴 생각이 없고 데이터가 약하다는 믿음이 있었기 때문에 커팅을 동반한 SPFA를 사용해서 뚫었습니다.
  • (00-38 - 00:40) E를 읽었는데 이상한 풀이만 생각나서 F로 넘어갔습니다.
  • (00:40 - 00:51) 누가봐도 2-SAT문제입니다. 위에서 설명한대로 2-SAT을 잘 쓰면 되는데, 저는 그 방법을 몰라서 2-SAT + 그리디라는 이상한 풀이를 짰습니다. 왠지 모르게 AC가 나와서 그냥 넘어갔는데, 끝나고 출제자에게 들어보니 데이터가 뚫렸다고 합니다.
  • (00:51 - 01:28) Fenwick Tree와 Parametric Search를 이용한 $O(N \log^2 N)$ 풀이가 나왔습니다. $N \leq 500,000$이라서 더 빠른 풀이가 있을지 꽤 오래 고민했지만 생각나지 않아서 그냥 로그제곱 짜서 제출했습니다. 코딩 미스로 2틀 후 AC
  • (01:28 - 01:46) E를 다시 읽어보니 degree에 이상한 조건이 붙어있는 그래프에서 해밀턴 사이클을 찾는 문제였습니다. 구글에 hamiltonian cycle degree condition를 검색했더니 풀이가 나와서 그대로 구현했습니다.
  • (01:46 - 02:30) 다 풀고 44분이 남았길래 강아지랑 산책하러 나갔습니다.

6문제 중에 2문제를 뚫었습니다.
2년 전 선린정올에서도 어떤 선배가 데이터 뚫어서 만점받고 1등했는데, 이렇게 보니 데이터를 뚫는 것은 선린정올 금상의 기본소양인 것 같습니다.

졸업하기 전에 천하제일 코딩대회, 선린정올, 프로그래밍 경시, 수학 경시 한 번씩은 1등 해봤으니 소원은 다 이뤘습니다. 이제 대학만 가면 되겠네요.