다양한 경우의 수 세기

작성일 | In

0. 목차

  1. 기본 지식
  2. 카탈란 수
  3. 집합의 분할
  4. 자연수의 분할
  5. 교란 순열
  6. 조합론의 12정도

1. 기본 지식

본론으로 들어가기 전에 중학교와 고등학교에서 배운 내용을 아주 빠르게 복습하고 넘어갑시다.

1-1. 순열, 중복 순열, 조합, 중복 조합

$n$개의 원소 중 중복 없이 $k$개의 원소를 선택해서 나열하는 방법의 수는 $n \times (n-1) \times \cdots \times (n-k+1) = \frac{n!}{(n-k)!}$가지입니다. 각 상자에 최대 1개의 공이 들어가도록 $k$개의 공을 $n$개의 상자에 분배하는 방법의 수라고 생각할 수도 있습니다. 흔히 고등학교에서는 이것을 순열이라고 부르고, $_nP_k$와 같은 기호로 나타냈습니다.

중복 순열은 위 문제에서 중복이 없어야 한다는 조건을 제거한 것인데, 중복을 허용해서 $k$개의 원소를 선택하고 나열하는 방법의 수는 $n^k$으로 계산할 수 있습니다. $k$개의 공을 $n$개의 상자에 자유롭게 분배하는 방법의 수라고 생각할 수도 있습니다.

조합은 $n$개의 원소 중 중복 없이 $k$개의 원소를 선택하는 방법의 수를 의미하고, $\frac{n\times(n-1)\times\cdots\times(n-k+1)}{k\times(k-1)\times\cdots\times1} = \frac{n!}{(n-k)!k!}$으로 계산할 수 있습니다. 고등학교에서는 주로 $_nC_k$라는 기호를 사용하고, 대학교에서는 주로 $n \choose k$라는 표기를 사용합니다. 이 글에서는 $n \choose k$라는 기호를 사용하겠습니다.

$n$개의 원소 중 중복 없이 $k$개의 원소를 선택하는 것은 (1) $n$번 원소를 선택한 다음 $1\sim n-1$번 원소 중 $k-1$개를 선택하는 것과 (2) $n$번 원소를 선택하지 않고 $1\sim n-1$번 원소 중 $k$개를 선택하는 것으로 나눠서 생각할 수도 있습니다. 따라서 ${n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}$라는 점화식을 이용해 계산할 수도 있습니다. 또한, $n$개의 원소 중 $k$개를 선택하는 것은 선택하지 않을 $n-k$개를 선택하는 것이라고 생각할 수 있으므로 ${n \choose k} = {n \choose n-k}$가 성립한다는 것을 알 수 있습니다.

조합을 사용하는 대표적인 문제로 격자 상의 최단 경로 개수를 세는 문제가 있습니다. 격자에서 $(0, 0)$에서 출발해 $(n, m)$으로 이동하는 최단 경로의 개수는 $\frac{(n+m)!}{n!m!} = {n+m \choose n}$으로 계산할 수 있고, 이는 $n+m$번의 이동 중 세로 방향으로 이동할 $n$번의 위치를 선택하는 것과 동일합니다. 이 문제는 뒤에서 카탈란 수를 설명할 때 다시 등장하니 꼭 알고 있어야 합니다.

중복 조합은 위 문제에서 중복이 없어야 한다는 조건을 제거한 것입니다. 중복 조합 문제는 $k$개의 원소가 들어갈 자리를 만든 다음 $n-1$개의 칸막이를 원소와 원소 사이에 배치해서, 첫 번째 칸막이 바로 전까지는 1번 원소, 첫 번째 칸막이와 두 번째 칸막이 사이에는 2번 원소, $n-1$번째 칸막이 이후에는 $n$번 원소를 배치하는 것으로 생각할 수 있습니다. 이는 $k+(n-1)$개의 원소 중 $n-1$개의 원소를 골라 칸막이로 교체하는 것이라고 생각할 수 있고, 따라서 $n+k-1 \choose n-1$로 계산할 수 있습니다. 고등학교에서는 $_nH_k$라는 기호를 사용했습니다.

1-2. 포함 배제의 원리

여러 개의 집합이 주어졌을 때 합집합의 크기를 구하는 방법에 대해 알아봅시다. 집합 $A, B$가 주어졌을 때 $\vert A \cup B \vert$는 $\vert A \vert + \vert B \vert - \vert A \cap B \vert$로 계산할 수 있고, 집합이 3개 주어진다면 $\vert A\cup B\cup C \vert$는 $\vert A \vert + \vert B \vert + \vert C \vert - \vert A\cap B\vert - \vert B\cap C\vert - \vert C \cap A \vert + \vert A \cap B \cap C \vert$를 이용해 계산할 수 있습니다. 이를 일반화하면 홀수 개의 집합을 교집합한 것의 크기는 더하고, 짝수 개를 교집합한 것의 크기는 빼는 방식으로 계산할 수 있다는 것을 알 수 있습니다. 수식으로는 $\vert \bigcup_{i=1}^{n} A_i \vert = \sum_{I \subset [n]} (-1)^{\vert I\vert-1} \vert \bigcap_{i\in I} A_i \vert$와 같이 나타낼 수 있습니다.

1-3. 이항 계수의 빠른 계산

${n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}$를 이용하면 $n, k \leq N$일 때의 이항 계수를 $O(N^2)$ 시간에 계산할 수 있습니다. 하지만 이항 계수를 적당한 정수 $M$으로 나눈 나머지를 구하는 것은 $O(N^2)$보다 빠르게 계산할 수 있고, 온라인 저지에서 문제를 풀 때는 주로 이런 방법을 요구합니다.

  • $N < M$, $M$은 소수: 전처리 $O(N + \log M)$, 쿼리 $O(1)$
  • $M$은 소수: 전처리 $O(M + \log M)$, 쿼리 $O(\log N)$
  • $M$은 소수의 거듭제곱($M=p^e$): 전처리 $O(p^e)$, 쿼리 $O(\log n + \log p)$
  • 조건 없음: 소인수분해 후 $M=p^e$인 문제를 해결한 뒤, 중국인의 나머지 정리를 이용해서 합치면 됨

위 네 가지 방법은 (여기)에 있는 슬라이드에서 자세한 설명을 확인할 수 있습니다. 첫 번째 방법만 알아도 연습 문제를 푸는 데 큰 지장은 없습니다.

2. 카탈란 수

2-1. Dyck Path

Dyck path 문제란, 격자에서 $(0, 0)$에서 $(n, n)$으로 이동할 때, 주대각선($y=x$ 직선)을 넘어가지 않는 경로의 개수를 구하는 문제입니다. 편의상 $(0, 0)$을 왼쪽 아래, $(n, n)$을 오른쪽 위에 있는 점이라고 정의합시다. 이러한 경로의 개수는 전체 경로의 개수에서 $y=x$를 뚫고 지나가는 경로의 개수를 빼서 구할 수 있습니다. 즉, $2n \choose n$에서 $y=x$를 뚫고 지나가는 경로의 개수를 뺀 값을 계산하면 됩니다. $y=x$ 직선을 뚫고 가는 직선의 개수를 구하는 방법을 알아봅시다.

$y=x$를 뚫고 올라가는 경로는 항상 $y=x+1$ 직선 위의 점을 한 번 이상 지납니다. 이런 경로마다 처음으로 $y=x+1$과 만나는 점 이후의 모든 이동을 반전시키면, $y=x$를 뚫고 가는 모든 경로는 $(n-1, n+1)$에 도착하게 됩니다.

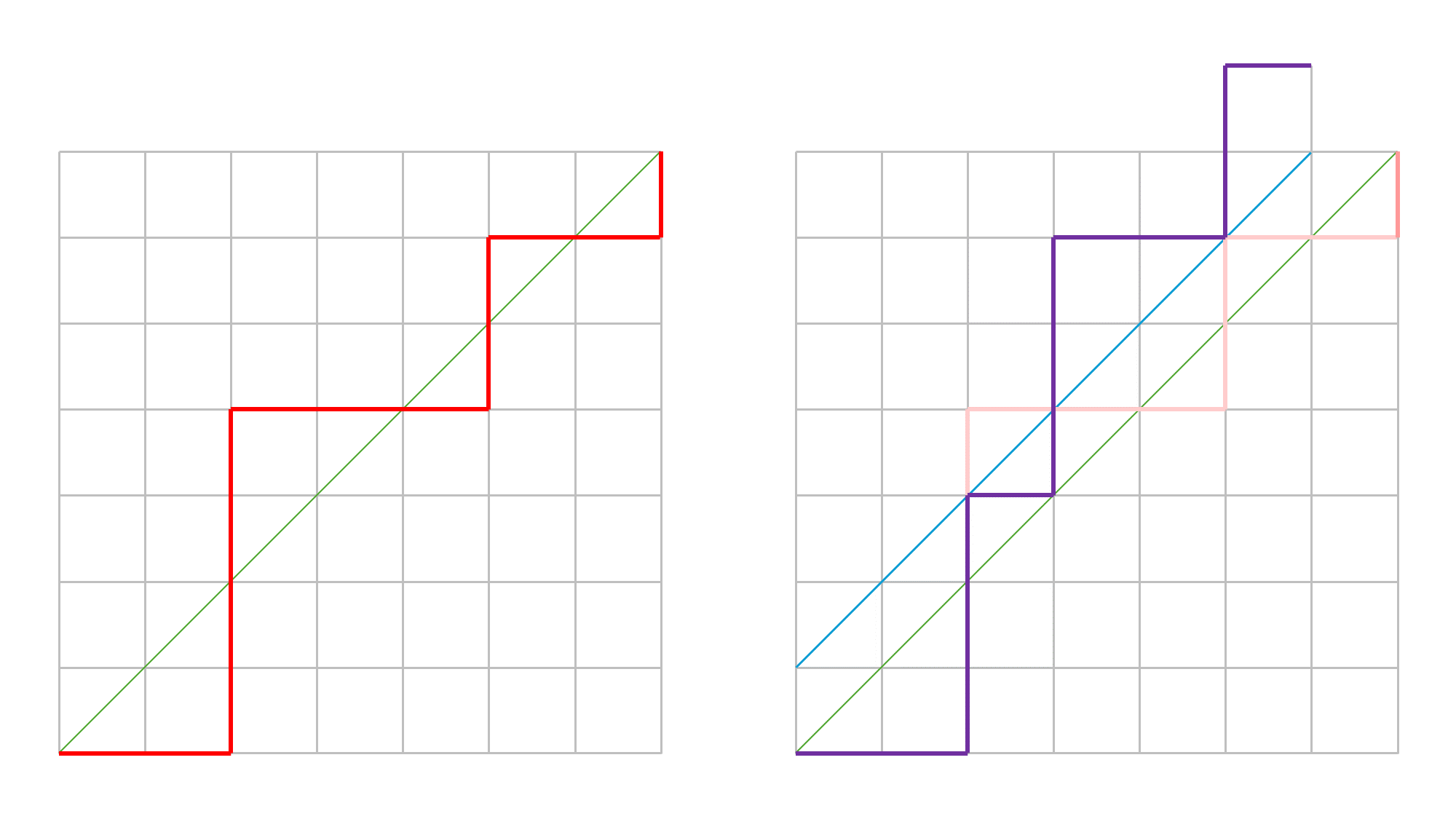
$y=x$를 뚫고 가는 모든 경로는 $(0, 0)$에서 $(n-1, n+1)$까지 가는 경로와 일대일 대응시킬 수 있고, 따라서 Dyck path 의 개수는 ${2n \choose n} - {2n \choose n+1}$로 계산할 수 있습니다. 이때 ${2n \choose n+1} = \frac{n}{n+1}{2n \choose n}$이므로 $\frac{1}{n+1}{2n \choose n}$으로도 계산할 수 있습니다.

원점을 제외하고 처음으로 $y=x$ 직선과 만나는 점을 기준으로 나눠서 생각하면 점화식도 유도할 수 있습니다. $(0, 0)$에서 $(n, n)$으로 이동하는 Dyck path의 개수를 $C_n$이라고 정의합시다. 경로가 원점을 제외하고 $y=x$와 처음 만나는 점이 $(k, k)$라고 하면, $(0, 0)$에서 $(k, k)$까지 가는 경로의 개수는 $C_{k-1}$, $(k, k)$에서 $(n, n)$으로 가는 경로의 개수는 $C_{n-k}$로 계산할 수 있습니다. 아래 그림은 $n = 7$, $k = 3$인 상황입니다.

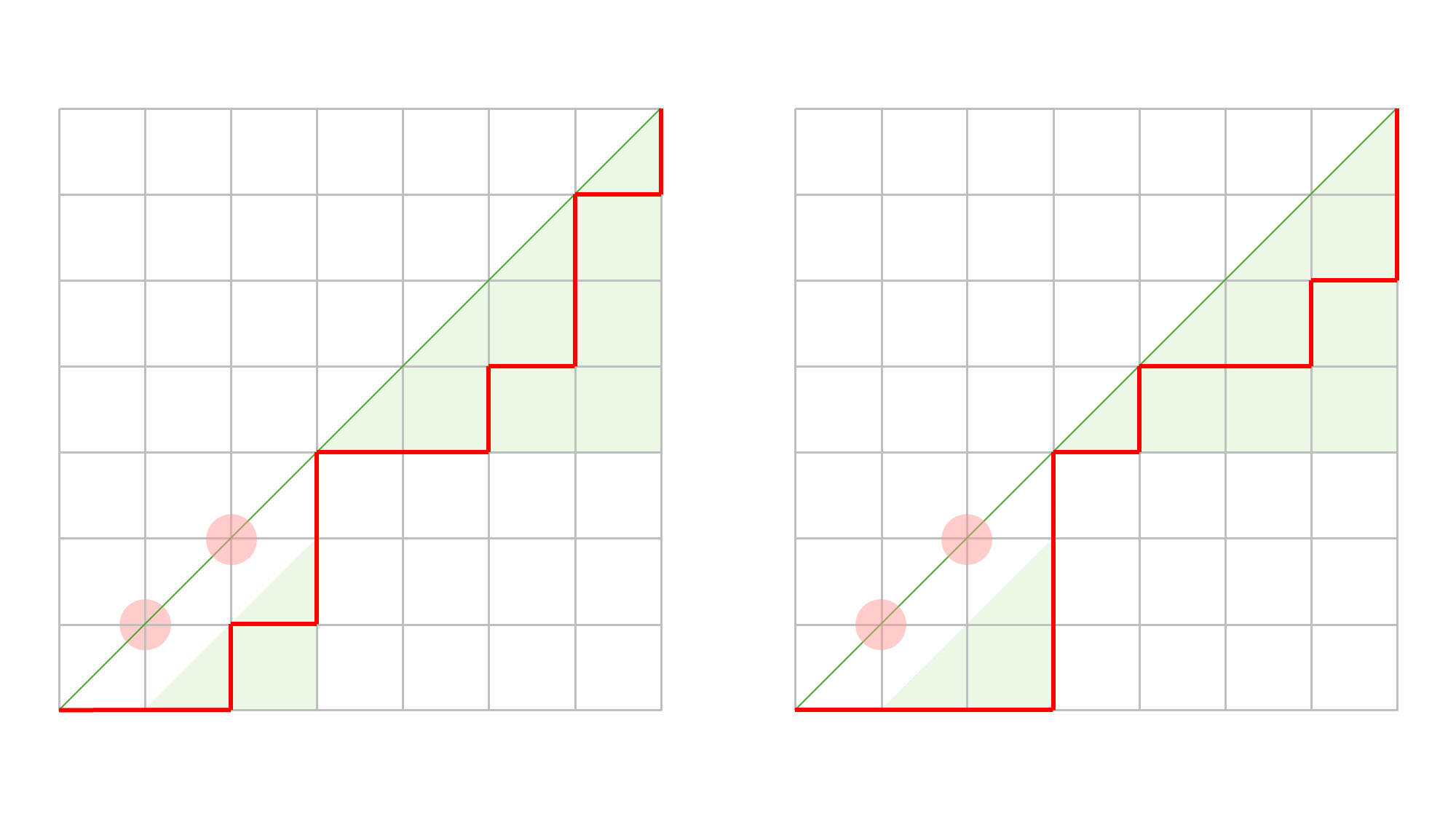
따라서 $C_n = \sum_{k=1}^n C_{k-1}C_{n-k} = \sum_{k=0}^{n-1} C_kC_{n-k-1}$이라는 점화식을 얻을 수 있습니다. 이렇게 정의되는 수열 $C_n$을 카탈란 수라고 부릅니다.

생성 함수를 이용하면 $\sum_{n=0}^\infty C_nx^n=\frac{1-\sqrt{1-4x}}{2x}$를 이용해 $C_0, C_1, \cdots, C_n$를 $O(n \log n)$에 계산할 수 있지만… 글의 범위를 벗어나므로 설명을 생략하겠습니다.

2-2. 카탈란 수로 해결할 수 있는 문제들

여는 괄호 $n$개와 닫는 괄호 $n$개로 구성된 올바른 괄호 문자열는 총 $C_n$가지가 있습니다. 여는 괄호와 닫는 괄호를 각각 오른쪽 이동과 위쪽 이동으로 생각하면 dych path 문제로 바꿀 수 있습니다. 또한, 리프 정점이 $n+1$개이고 모든 정점의 자식이 0개 또는 2개인 full binary tree의 개수는 $C_n$과 동일합니다. 수식 트리를 $n+1$개의 항이 있는 수식에 $n$쌍의 괄호를 씌워 이항 연산자를 적용하는 경우의 수와 동일하기 때문입니다. 다르게 이야기하면 내부 정점(internal node)가 $n$개인 full binary tree의 개수가 $C_n$이라고 생각할 수도 있습니다.

볼록 $n+2$각형에 $n-1$개의 대각선을 그려서 $n$개의 삼각형으로 분할하는 방법의 수도 $C_n$입니다. 다각형의 한 변을 고정한 뒤, 그 변을 밑변으로 하는 삼각형을 만들기 위해 대각이 될 꼭짓점을 선택하는 상황을 생각해 봅시다. $n+2$각형에서 한 변을 고정했을 때 대각이 될 수 있는 꼭짓점의 후보는 $n$개이며, 그중 $k(1 \leq k \leq n)$번째 점을 선택하면 도형은 삼각형 하나, 후보가 $k-1$개인 볼록 $k+1$각형, 후보가 $n-k$개인 볼록 $n-k+2$각형으로 분할됩니다. 따라서 $C_n = \sum_{k=1}^{n} C_{k-1}C_{n-k} = \sum_{k=0}^{n-1}C_kC_{n-k-1}$이라는 점화식을 얻을 수 있고, 이는 카탈란 수의 점화식과 동일합니다.

이밖에도 카탈란 수를 이용해 풀 수 있는 문제가 많이 있는데, 아래에 있는 연습 문제를 풀어보면서 카탈란 수에 어떻게 대응시킬 수 있을지 고민해 보는 것을 추천합니다.

2-3. 카탈란 삼각형

카탈란 삼각형 $C(n, k)$는 여는 괄호 $n$개와 닫는 괄호 $k(\leq n)$개로 구성된 문자열 중, 모든 닫는 괄호가 여는 괄호와 매칭된 문자열의 개수를 나타냅니다. $k < n$이면 여는 괄호와 매칭되는 닫는 괄호가 존재할 수도 있지만, 모든 닫는 괄호는 여는 괄호와 매칭되어야 합니다. Dyck path 문제와 비슷한 방법을 이용해 $C(n, k) = {n+k \choose k} - {n+k \choose k-1}$로 계산할 수 있으며, $C(n, k) = \frac{n-k+1}{n+1}{n+k \choose k}$도 성립합니다.

Wikipedia에 따르면 $C(n, k) = \sum_{i=0}^{k} C(n-1, i) = \sum_{i=k}^{n} C(i, k-1)$이 성립하고, 따라서 $C(n, k) = C(n, k-1) + C(n-1, k)$도 성립한다고 합니다.

3. 집합의 분할

3-1. 제2종 스털링 수

제2종 스털링 수는 $n$개의 원소를 $k$개의 부분 집합으로 분할하는 경우의 수를 의미하며, 주로 ${n \brace k}$ 또는 $S(n, k)$로 나타냅니다. 이때, 각 부분 집합은 공집합이 아니고, 부분 집합 간의 교집합이 존재하면 안 됩니다. 예를 들어 ${1, 2, 3}$을 2개의 부분 집합으로 분할하는 방법은 ${1, 2} \cup {3}$, ${2, 3}\cup {1}$, ${3, 1} \cup {2}$로 3가지이므로 ${3 \brace 2} = 3$입니다. $n \brace k$를 계산하는 것은 $n$번 원소가 들어가는 집합을 기준으로 생각해 보면 아래 두 가지 경우로 나눠서 계산할 수 있다는 것을 알 수 있습니다.

  1. $n-1$개의 원소를 $k-1$개의 부분 집합으로 분할한 뒤, 새로운 집합을 만들어서 $n$번 원소를 삽입
  2. $n-1$개의 원소를 $k$개의 부분 집합으로 분할한 뒤, $n$번 원소를 $k$개의 부분 집합 중 한 곳에 삽입

따라서 ${n \brace k} = {n-1 \brace k-1} + {n-1 \brace k} \times k$ 를 이용해 계산할 수 있습니다.

3-2. 벨 수

벨 수는 $n$개의 원소를 분할하는 경우의 수를 의미하며, 주로 $B_n$으로 나타냅니다. 정의에서 알 수 있듯이 벨 수는 $B_n = \sum_{k=0}^n {n \brace k}$로 계산할 수 있습니다. 이때, ${0 \brace 0} = B_0 = 1$로 맞추기 위해서 $k$를 $0$부터 더합니다.

점화식을 이용해 벨 수를 계산할 수도 있습니다. $n$번 원소를 포함하는 집합의 크기에 주목합시다. $n$번 원소를 포함하는 집합의 크기가 $k$가 되도록 분할하기 위해서는 $n$번 원소를 제외한 나머지 $n-1$개의 원소 중 $k-1$개를 선택한 다음, 이 집합에 포함되지 않은 $n-k$개의 원소를 적절히 분할하면 됩니다. 따라서 $B_n = \sum_{k=1}^{n} {n-1 \choose k-1}B_{n-k}$ $= \sum_{k=0}^{n-1} {n-1 \choose k}B_{n-k-1}$ $=\sum_{k=0}^{n-1} {n-1 \choose n-k-1}B_{n-k-1}$ $= \sum_{k=0}^{n-1} {n-1 \choose k}B_k$ 라는 점화식을 얻을 수 있고, $B_0, B_1, \cdots, B_n$을 $O(n^2)$ 시간에 전처리할 수 있습니다. 생성 함수를 이용하면 $\sum_{n=0}^\infty \frac{B_n}{n!}x^n = e^{e^x-1}$를 이용해 $O(n \log n)$에 계산할 수 있지만 글의 범위를 벗어나므로 설명을 생략하겠습니다.

3-3. 제2종 스털링 수의 일반항

포함 배제의 원리를 이용하면 제2종 스털링 수의 일반항을 구할 수 있습니다. 처음에는 $n$명의 사람을 $k$개의 방에 자유롭게 집어넣는 것에서 시작합니다. 즉, 공집합을 허용하고, $k$개의 부분 집합을 서로 구분하는 상황에서 시작합니다. 이런 배정은 총 $k^n$가지가 있습니다. 여기에서 빈방이 1개 이상 생기는 모든 배정의 개수를 빼면 되고, 이는 ($r$개의 빈방을 고정하는 경우의 수) * ($k-r$개의 방에 $n$명의 사람을 집어넣는 경우의 수) $= {k\choose r}(k-r)^n$을 이용해 포함 배제를 하면 계산할 수 있습니다.

식으로 나타내면 $k!{n \brace k} = k^n + \sum_{r=1}^{k} (-1)^r{k \choose r}(k-r)^n = \sum_{r=0}^{k} (-1)^r{k \choose r}(k-r)^n$ 이 되고, ${k \choose r} = {k \choose k-r}$이라는 것을 이용하면 $k!{n \brace k} = \sum_{r=0}^{k} (-1)^r{k \choose k-r}(k-r)^n = \sum_{r=0}^{k} (-1)^{k-r}{k \choose r}r^n$으로 나타낼 수 있습니다. 제2종 스털링 수는 집합을 구분하지 않기 때문에 $n \brace k$는 앞에서 구한 식을 $k!$으로 나눈 값인 $\frac{1}{k!}\sum_{r=0}^{k}(-1)^{k-r}{k \choose r}r^n = \frac{(-1)^k}{k!}\sum_{r=0}^{k} (-1)^{r}{k \choose r}r^n$입니다.

3-4. 제1종 스털링 수

부호 없는 제1종 스털링 수는 $n$개의 원소를 $k$개의 방향 있는 사이클로 분할하는 경우의 수를 의미하며, 주로 $\begin{bmatrix} n \ k \end{bmatrix}$로 나타냅니다. 순열의 사이클 분할을 생각하면, $\sum_{k=1}^{n} \begin{bmatrix} n \ k \end{bmatrix} = n!$ 임을 알 수 있습니다. 제1종 스털링 수도 제2종 스털링 수와 같이 점화식을 이용해 계산할 수 있는데, $n$번 원소가 들어갈 위치를 기준으로 생각해 보면 아래 두 가지 경우로 나눌 수 있다는 것을 알 수 있습니다.

  1. $n-1$개의 원소로 $k-1$개의 사이클을 만든 뒤, $n$번 원소 혼자 있는 사이클을 생성
  2. $n-1$개의 원소로 $k$개의 사이클을 만든 뒤, 만들어진 $n-1$개의 간선 중 하나를 골라서 사이에 $n$번 원소 삽입

따라서 $\begin{bmatrix} n \ k \end{bmatrix} = \begin{bmatrix} n-1 \ k-1 \end{bmatrix} + \begin{bmatrix} n-1 \ k \end{bmatrix} \times (n-1)$이라는 점화식을 얻을 수 있습니다.

4. 자연수의 분할

4-1. 영 다이어그램과 자연수 분할

$\lambda = (\lambda_1, \lambda_2, \cdots, \lambda_k)$가 아래 조건을 만족할 때 $\lambda$를 $N$의 자연수 분할이라고 부릅니다.

  1. $\lambda_i$는 양의 정수
  2. $\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_n > 0$
  3. $\sum_{i=1}^k \lambda_i = N$

$N$의 자연수 분할 $\lambda = (\lambda_1, \lambda_2, \cdots, \lambda_k)$가 주어지면 $\lambda$를 이용해 $k$개의 행으로 구성되어 있고 $i$번째 행에 $\lambda_i$개의 칸이 있는, 총 $n$칸짜리 영 다이어그램을 만들 수 있습니다. 예를 들어 9의 자연수 분할 $(4, 3, 1, 1)$의 영 다이어그램은 다음과 같습니다.

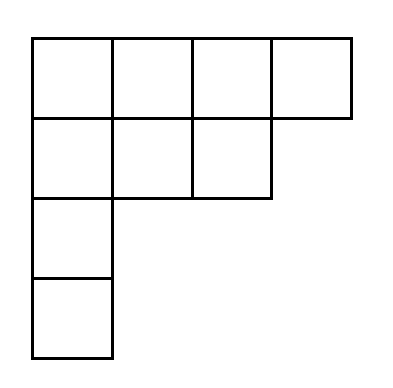
조합론에서 영 다이어그램은 많은 의미를 갖고 있지만, 이 글의 범위를 벗어나고 아직 저도 잘 모르기 때문에 생략합니다.

4-2. 분할 수의 계산

$P_k(n)$ 또는 $P(n, k)$는 자연수 $n$을 순서를 고려하지 않고 $r$개의 자연수의 합으로 나타내는 경우의 수를 의미합니다. 행이 $k$개인 $n$칸짜리 영 다이어그램의 가짓수라고 생각해도 무방합니다. $P(n, k)$의 점화식은 영 다이어그램의 마지막 행의 길이를 기준으로 생각하는 것이 편합니다. 행이 $k$개인 $n$칸짜리 영 다이어그램을 만드는 것은 아래 두 가지 경우로 나눠서 생각할 수 있습니다.

  1. (마지막 행의 길이가 1인 경우) 행이 $k-1$개인 $n-1$칸짜리 영 다이어그램을 만든 뒤, 밑에 길이가 1인 행 하나 추가
  2. (마지막 행의 길이가 2 이상인 경우) 행이 $k$개인 $n-k$칸짜리 영 다이어그램을 만든 뒤, 각 행의 길이를 1씩 증가

따라서 $P(n, k) = P(n-1, k-1) + P(n-k, k)$라는 점화식을 얻을 수 있습니다. 특이하게도 자연수 $n$을 분할하는 방법의 수 $P(n) = \sum_{k=1}^{n} P(n, k)$를 $O(N \sqrt N)$ 시간에 계산할 수 있는 점화식이 두 가지 있는데, 궁금하신 분들은 글 하단에 있는 링크를 참고하시길 바랍니다.

5. 교란 순열

5-1. 교란 순열의 점화식

교란 순열 또는 완전 순열이란 모든 $1 \leq i \leq n$에 대해 $\pi(i) \neq i$를 만족하는 길이 $n$짜리 순열 $\pi$를 의미합니다. 주로 $D_n$이나 $!n$ 으로 표기합니다. $\pi(n)$의 값을 기준으로 생각하면 어렵지 않게 $D_n$의 점화식을 유도할 수 있습니다. $n$번째 위치에 $n-1$번 원소가 들어간 상황, 즉 $\pi(n) = n-1$인 경우를 생각해 봅시다.

$n$번 원소는 $\pi(1), \pi(2), \cdots, \pi(n-1)$ 중 원하는 자리를 골라 들어갈 수 있습니다. 만약 $n$번 원소가 $n-1$번째 자리에 들어갔다면($\pi(n-1)=n$) 1번 원소부터 $n-2$번 원소까지를 적절히 배치하는 것으로 교란 순열을 만들 수 있습니다. 따라서 이 경우에는 $D_n$에 $D_{n-2}$ 만큼 기여합니다.

반대로 $n$번 원소가 $n-1$번째 자리가 아닌 다른 자리에 들어간 상황, 즉 $\pi(i)=n, i < n-1$ 인 경우에는 $n$번 원소에게 $n-1$이라는 가면을 임시로 씌워준 다음, $1, 2, \cdots, n-2, n$번 원소를 이용해 교란 순열을 만드는 것으로 $\pi(i) = n, i < n-1$은 모든 경우를 확인할 수 있습니다. 따라서 이 경우에는 $D_n$에 $D_{n-1}$ 만큼 기여합니다.

$\pi(n)$에 $n-1$이 아닌 $1, 2, \cdots, n-2$가 들어가는 경우도 동일한 방법으로 계산할 수 있고, 각각은 모두 $D_n$에 $D_{n-2} + D_{n-1}$ 만큼 기여합니다. 따라서 $D_n = (n-1)(D_{n-1} + D_{n-2})$ 라는 점화식을 얻을 수 있습니다.

5-2. 교란 순열의 일반항

점화식을 적절히 정리하면 $D_n$의 일반항도 얻을 수 있습니다. $D_n = (n-1)(D_{n-1} + D_{n-2}) = (n-1)D_{n-1} + (n-1)D_{n-2}$에서 시작합시다.
$nD_{n-1}$을 왼쪽으로 넘기면 $D_n - nD_{n-1} = -{ D_{n-1} - (n-1)D_{n-2} }$가 되고, $A_n = D_n - nD_{n-1}$로 정의하면 $A_n = -A_{n-1}$이 되어 $A$는 공비가 $-1$인 등비수열임을 알 수 있습니다. 이때, $A_1 = D_1 - D_0 = 0 - 1 = -1$이므로 $A_n = (-1)^n$입니다.

따라서 $A_n = D_n - nD_{n-1} = -A_{n-1} = (-1)^n$이고, 양변을 $n!$으로 나누면 $\frac{D_n}{n!} - \frac{D_{n-1}}{(n-1)!} = \frac{(-1)^n}{n!}$이 됩니다. $B_n = \frac{D_n}{n!}$으로 정의하면 $B_n - B_{n-1} = \frac{(-1^n)}{n!}$이라는 점화식을 얻을 수 있고, 이를 일반항으로 나타내면 $B_n = B_1 + \sum_{k=2}^{n} \frac{(-1)^k}{k!}$이고 $B_1 = \frac{D_1}{1!} = 0$이므로 $\frac{D_n}{n!} = \sum_{k=2}^{n} \frac{(-1)^k}{k!}$가 됩니다.

$\frac{(-1)^0}{0!} + \frac{(-1)^1}{1!} = 1 + (-1) = 0$이므로 $\frac{D_n}{n!} = \sum_{k=0}^n \frac{(-1)^k}{k!}$으로 써도 무방합니다. 따라서 $D_n = n! \sum \frac{(-1)^k}{k!}$이라는 일반항을 얻을 수 있습니다. 이때 $e^x$의 테일러 전개를 생각해 보면, $\frac{D_n}{n!}$의 일반항은 $e^x = \sum_{k=0}^\infty \frac{x^k}{k!}$에서 $x = -1$을 대입한 꼴이기 때문에, $\lim_{n\rightarrow \infty} \frac{D_n}{n!} = \frac{1}{e}$라는 것도 알 수 있습니다.

포함 배제의 원리를 이용해도 동일한 일반항을 유도할 수 있습니다. $n$개의 원소를 나열하는 방법 $n!$가지 중 $\pi(i)=i$인 $i$의 개수가 $k$ 이상인 순열이 $\frac{n!}{k!}$이라는 사실을 이용하면 $D_n = \sum_{k=0}^{n} (-1)^k \times \frac{n!}{k!} = n! \sum_{k=0}^n \frac{(-1)^k}{k!}$을 얻을 수 있습니다.

6. 조합론의 12정도

12정도는 $n$개의 원소를 $k$개의 집합으로 분할하는($n$개의 공을 $k$개의 상자에 넣는) 방법을 상황에 따라 분류한 표입니다. $[\text{cond}]$는 아이버슨 괄호로, 대괄호 안에 있는 조건이 참이면 $1$, 거짓이면 $0$을 나타냅니다.

동치 관계 \ 함수 조건 조건 없음 단사 함수(상자에 공 최대 1개) 전사 함수(상자에 공 최소 1개)
함수 일치 $k^n$ $_kP_n = k!/(k-n)!$ $k! \times {n \brace k}$
정의역의 순열 무시(공 구별 X) $_kH_n = {n+k-1 \choose n}$ $k \choose n$ $n-1 \choose n-k$, 단, $n=k=0$이면 $1$
공역의 순열 무시(상자 구별 X) $\sum_{r=1}^{k} {n \brace r}$ $[n \leq k]$ $n \brace k$
둘 다 무시(모두 구별 X) $P(n+k, k)$ $[n \leq k]$ $P(n, k)$

더 공부할 거리

연습 문제