팀 연습
굳이 예선 준비를 해야 하나 싶지만… ICPC WF와 서울 리저널 사이의 간격이 너무 짧아서 리저널 연습을 미리 한다는 느낌으로 연습했습니다. 연습은 각자 집에서 진행했으며, 음성 채팅을 하면서 두 명 이상의 사람이 동시에 키보드를 잡지 않도록 제한했습니다.
까먹지 않기 위해서 제가 푼 문제만 간단하게 정리합니다. 스포일러 주의!
(10/11) ECNA 2022 (3시간)
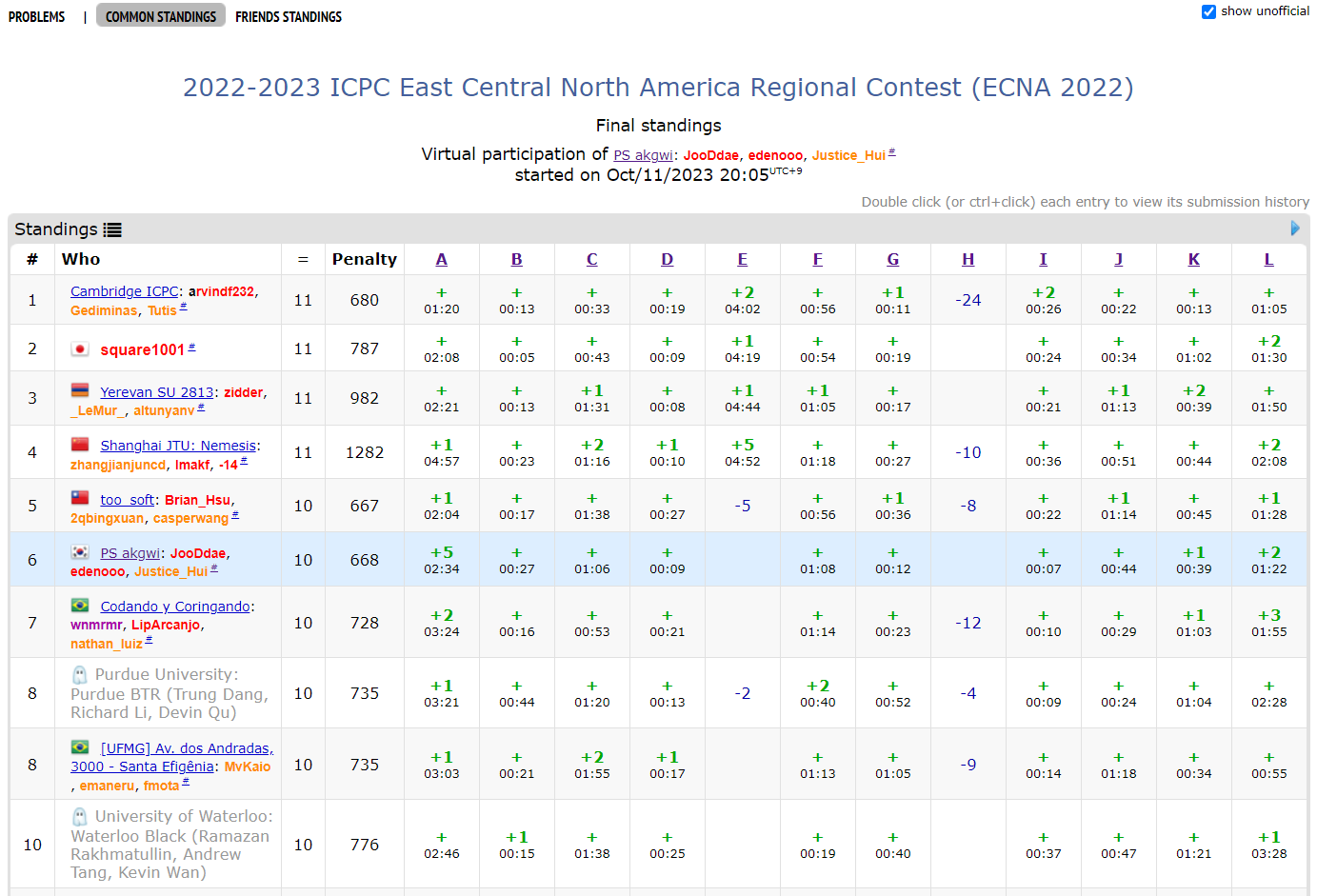
링크(Codeforces): 2022-2023 ICPC East Central North America Regional Contest (ECNA 2022)
링크(BOJ): ecna2022
총평: solved.ac 기준 골드 이하의 쉬운 문제가 너무 많아서 우리 팀에게는 별로 맞지 않는 셋이었다. 최근에 외국인들 팀노트를 구경하면서 포커 구현 코드가 있는 것을 보고 신기했던 기억이 있는데, 이 대회를 치고 나니 왜 그런 코드를 넣는지 이해가 된다. 한국인들은 윷놀이 구현체를 넣어야 하나?
A. A-Mazing Puzzle: 4차원 격자 그래프에서 최단 경로를 구한다는 생각은 쉽게 할 수 있다. 한숨 한 번 내쉬고 열심히 구현하면 된다.
C. Cribbage On Steroids: 패를 만드는 카드의 숫자들을 고정한 뒤, 그러한 숫자 조합을 만드는 경우의 수를 세면 된다. 15를 세는 게 어렵다고 생각할 수 있는데 P(15)가 별로 크지 않아서 그냥 브루트포스를 해도 된다.
D. Determining Nucleotide Assortments: Do you know prefix sum?
J. Simple Solitaire: 단순 구현
L. Which Warehouse?: Do you know assignment problem? 대회 중에는 팀원이 풀었다.
반성할 점: 문제 그림 확인하고 연습 셋 정하자.
(10/12) TOPC 2023 (3시간)
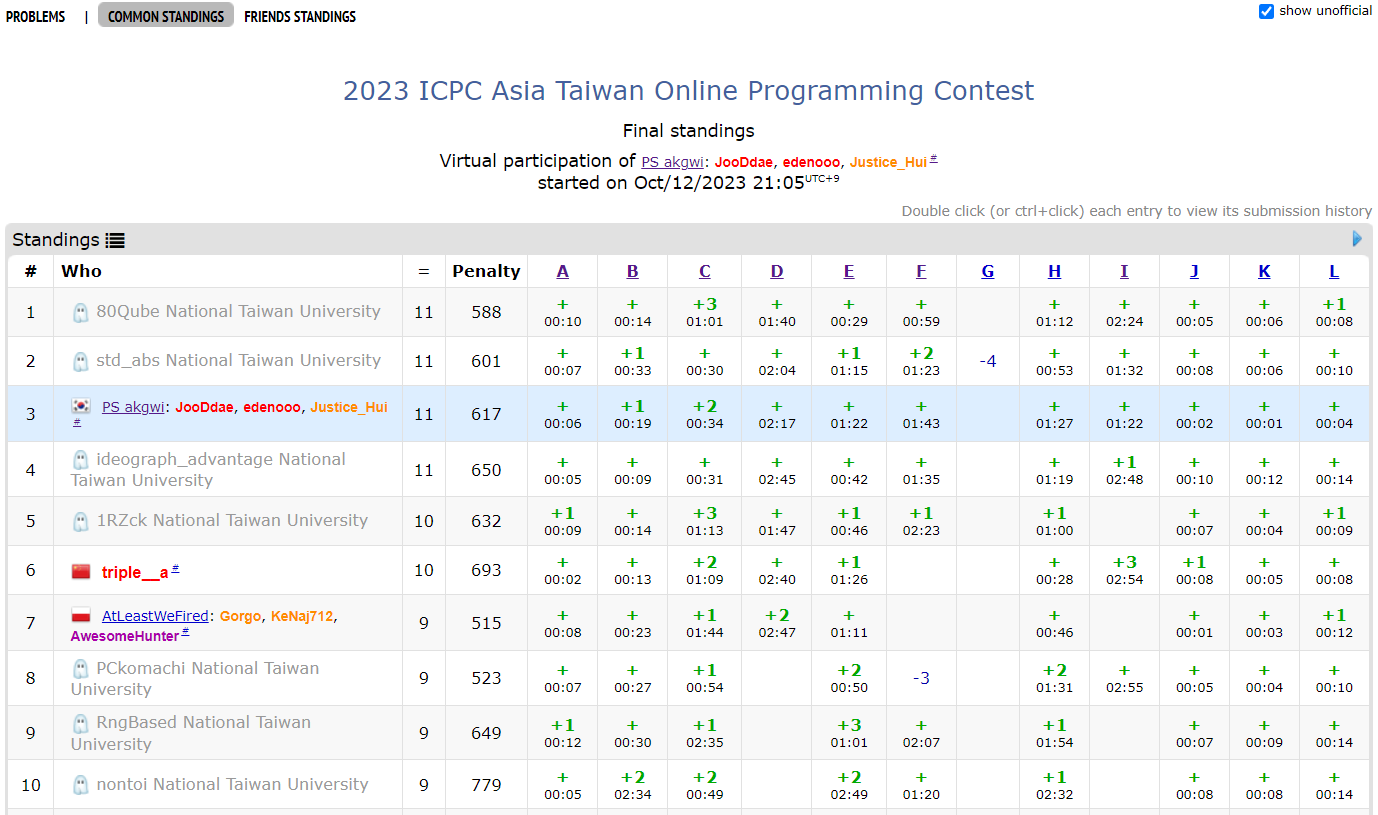
링크(Codeforces): 2023 ICPC Asia Taiwan Online Programming Contest
링크(BOJ): topc2023
총평: 서울 지역 예선 연습용으로 좋은 셋이다.
A. Advance to Taoyuan Regional: 지문 위에 있는 Category 관련 내용은 문제와 아무런 관련이 없는데 열심히 읽느라 시간을 날렸다. 날짜 계산하는 전형적인 브론즈 문제
C. Cutting into Monotone Increasing Sequence: 골드 3~4에 있을 것 같은 전형적인 DP 문제인데 왜 많이 안 풀렸는지 모르겠다. C++로 풀기 위해서는 int128을 사용하거나 귀찮은 예외 처리가 필요하다.
E. Exponentiation: 수식을 열심히 정리하다 보면, $D(0) = 2, D(1) = a, D(n)=a\times D(n-1) - D(n-2)$가 성립함을 알 수 있다. 따라서 $\begin{pmatrix}a&-1\1&0\end{pmatrix}^{\beta-1}\begin{pmatrix}a\2\end{pmatrix}$를 계산하면 $O(\log \beta)$ 시간에 문제를 해결할 수 있다.
F. Finding Bridges: 쿼리를 뒤에서부터 처리하면 간선이 추가될 때마다 단절선의 개수를 관리하는 문제가 된다. 추가하는 간선을 $e=(u,v)$라고 할 때, $u$와 $v$가 연결되어 있지 않으면 $e$는 단절선이 되고, 그렇지 않으면 $u$와 $v$를 잇는 경로 위에 있는 모든 간선이 더 이상 단절선이 아니게 된다. 따라서 HLD로 경로 업데이트를 하면 쿼리당 $O(\log^2 N)$에 해결할 수 있다.
반성할 점: 없다.
(10/13) SWERC 2016 (5시간)
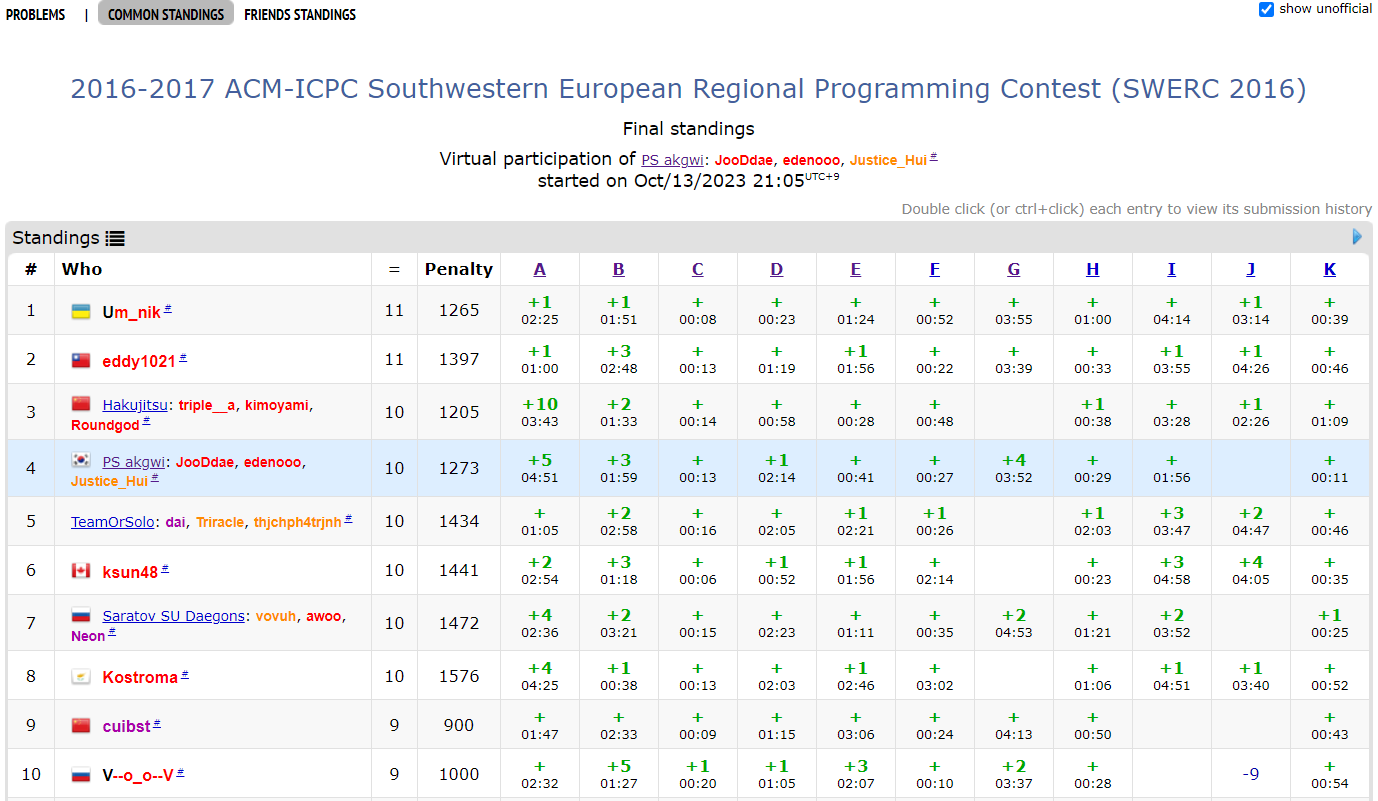
링크(Codeforces): 2016-2017 ACM-ICPC Southwestern European Regional Programming Contest (SWERC 2016)
링크(BOJ): swerc2016
총평: 서울 지역 예선 연습용으로 좋은 셋이다.
B. Bribing Eve: $ax+by$를 최대화하는 것은 좌표 평면 위에 점 $(x,y)$를 찍어놓고 기울기가 $-b/a$인 집선을 긋는 것과 같다. 따라서 이 문제는 원점을 지나는 기울기가 음수인 모든 직선을 보면서, 오른쪽 위에 있는 점의 최대/최소 개수를 구하는 문제라고 생각할 수 있다. 기울기가 같은 점 처리하는 게 조금 귀찮다. 같은 점이 여러 개 주어질 수 있음에 주의하자. 여기저기에서 많이 보이는 아이디어다.
C. Candle Box: 쉬운 문제
E. Passwords: 이미 BOJ에서 5번 정도 풀어봤던 것 같은 아호코라식 DP 문제다. $D(i, s) := $ 길이가 $i$이고 $s$번 state에서 끝나는 문자열의 개수를 계산하면 된다. solvedac에 #aho_corasick #dp *p1..d5를 검색(link)하면 비슷한 문제를 여러 개 풀어볼 수 있다.
G. Cairo Corridor: 그림만 봐도 즐겁다. corridor를 따는 건 쉬운데 minimal corridor인지 $O((NM)^2)$보다 빠르게 판별하는 것은 쉽지 않다. 처음에는 minimal corridor가 존재하면 그 그래프가 꽤 작을 것이라고 추측해서 완전 탐색 풀이를 제출했는데 TLE를 받았고, 중요해 보이는 정점 몇 개만 확인하는 방식으로 고쳐서 AC를 받았다. 일반적으로 degree가 2인 정점은 확인할 필요가 없지만, degree가 3인 정점과 인접한 정점은 확인해야 한다.
A. Within Arm’s Reach: 팀원이 의문의 런타임 에러로 고통받고 있길래 2줄 수정해서 AC 받아줬다. 실수 오차는 만악의 근원이다.
반성할 점: 문제 조건을 잘 읽자(B). 대회장에서 기하 구현할 때는 페어 코딩하는 게 좋을 듯(A). J는 다시 풀어봐야지…
(10/15) TOPC 2021 (개인, 3시간)
링크(Codeforces): 2021 ICPC Asia Taiwan Online Programming Contest
링크(BOJ): topc2021
총평: TOPC 2023 대회가 괜찮았어서 동아리 내부 ICPC 모의 대회 셋으로 2021년 대회를 골랐는데 이건 별로였다. 다이아 이상의 어려운 문제는 사전지식이 있으면 쉽게 풀 수 있고, 쉬운 문제는 나름의 함정이 있어서… 나쁜 셋은 아니지만 좋은 셋도 아니라고 생각한다.
풀이는 여기에서 확인할 수 있다.
A. Olympic Ranking: 쉬운 문제
B. Aliquot Sum: 쉬운 문제
C. A Sorting Problem: $A[B[i]] = i$인 배열 $B$를 만들면 inversion counting 문제가 된다.
D. Drunk Passenger: solvedac에서는 골드5라고 하는데 그것보다는 어려운 것 같다. DP로 풀거나 열심히 식 정리해서 풀거나…
E. Eatcoin: 쉬운데 BigInteger가 필요해서 별로인 문제
F. Flip: 전형적인 금광 세그 연습 문제
G. Garden Park: 가중치가 작은 간선부터 추가하면서 DP를 해도 되고, 아니면 그냥 뇌 비우고 센트로이드 분할을 해도 된다.
H. A Hard Problem: $(u,i) \neq (v,j)$ 조건만 없으면 전형적인 민컷 문제인데 저 조건이 있어서 NP-Hard가 되었다. $Q \leq 8$이니까 $(u,i)$를 소스에 붙이는 경우와 싱크에 붙이는 경우를 모두 확인해도 $2^8$가지밖에 안 돼서 시간 안에 문제를 해결할 수 있다.
I. ICPC Kingdom: graphic matroid와 colorful matroid의 최대 가중치 공통 독립 집합
J. JavaScript: 쉬운 문제
반성할 점: 없다.
(10/16) 2023 Brazil Subregional Contest (3시간)
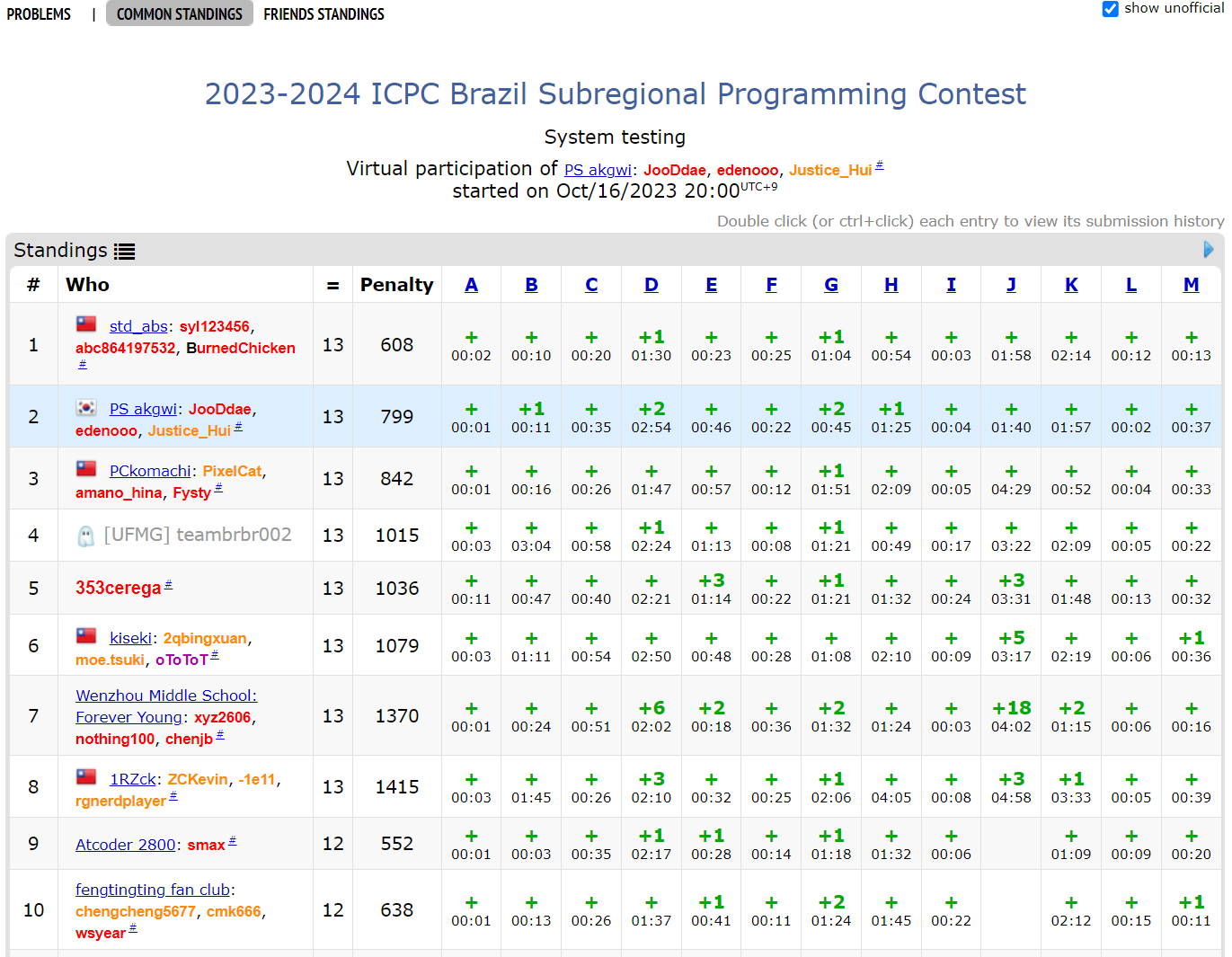
링크(Codeforces): 2023-2024 ICPC Brazil Subregional Programming Contest
링크(BOJ): latinp2023
총평: 잘 모르겠다. 내가 5문제를 풀긴 했는데 브론즈 1개 + 예전에 푼 문제 4개(골드, 플래티넘, 다이아, 루비 하나씩)라서 평가를 할 수가 없다. 5시간 연습하려고 했는데 3시간 만에 다 풀었다.
A. Amusement Park Adventure: 쉬운 문제
B. Best Fair Shuffles: BOJ 11232 Shuffles과 똑같은 문제
D. Detour: BOJ 1848 동굴 탐험과 똑같은 문제
G. Great Treaty of Byteland: 풀었던 기억은 있는데 어떤 문제인지 모르겠다. 평각을 허용하는 볼록 껍질의 꼭짓점 개수를 세면 된다.
J. Jumping to Victory: BOJ 1288 전쟁 - 국지전과 거의 똑같은데 $N \leq 10^5$인 문제. 보로노이 다이어그램을 $O(N \log N)$에 구할 수 있으면 그다음은 기하 구현을 열심히 해서 풀 수 있다.
반성할 점: D에서 동굴 탐험을 너무 늦게 떠올렸고, 전체적으로 구현 실수가 너무 많았다. Graham scan 구현에서 실수한 건 거의 2년 만인 것 같은데…
정리
팀 연습 도중에 발견한 문제가 몇 가지 있다. 가장 크리티컬한 문제는 팀노트 Convolution.cpp에 있는 multiply_mod 함수가 틀렸다는 것이고, 이밖에도 기하 관련 라이브러리가 부족하다는 문제점이 있다. 다음 달에 월드 파이널도 가야 해서 기하는 빨리 추가해야 한다.
팀노트에 들어간 거의 모든 코드를 내가 작성한 거라서 다른 팀원들이 사용법을 잘 모른다는 소소한 문제도 발견했다. 대회 때는 연습과 다르게 내가 옆에 앉아있을 거라서 큰 문제가 되진 않을 것 같지만, 그래도 매뉴얼을 만들어 놓으면 도움이 될 것 같다.