백준19022 Flow

작성일 | In

문제 링크

  • https://icpc.me/19022

사용 알고리즘

  • MCMF

풀이

수렴하지 않는 경우가 있다면 문제를 안 냈을 것 같으니 항상 수렴한다고 믿고 문제를 풀어봅시다.
$k$가 무한대로 발산하면 대부분의 유량이 사이클 안에 머물러 있고 일부만 싱크로 흘러가게 됩니다. 그러므로 일단 소스에서 유량을 최대한 많이 방출한 다음, 사이클 안에서 계속 도는 것을 최소화하는 방향으로 접근할 수 있습니다.
만약 어떤 정점 $u$에서 나간 유량이 $u$로 돌아오면 사이클이 만들어지고, 만약 사이클 밖으로 나갈 수 있었다면 $u$로 돌아오기 전에 밖으로 나갔을 것이기 때문에 $u \rightarrow \cdots \rightarrow u$ 꼴의 유량은 항상 사이클에 머물러 있는 유량입니다. 즉, $u \rightarrow \cdots \rightarrow u$ 꼴의 경로 개수를 최소화하는 문제가 됩니다.

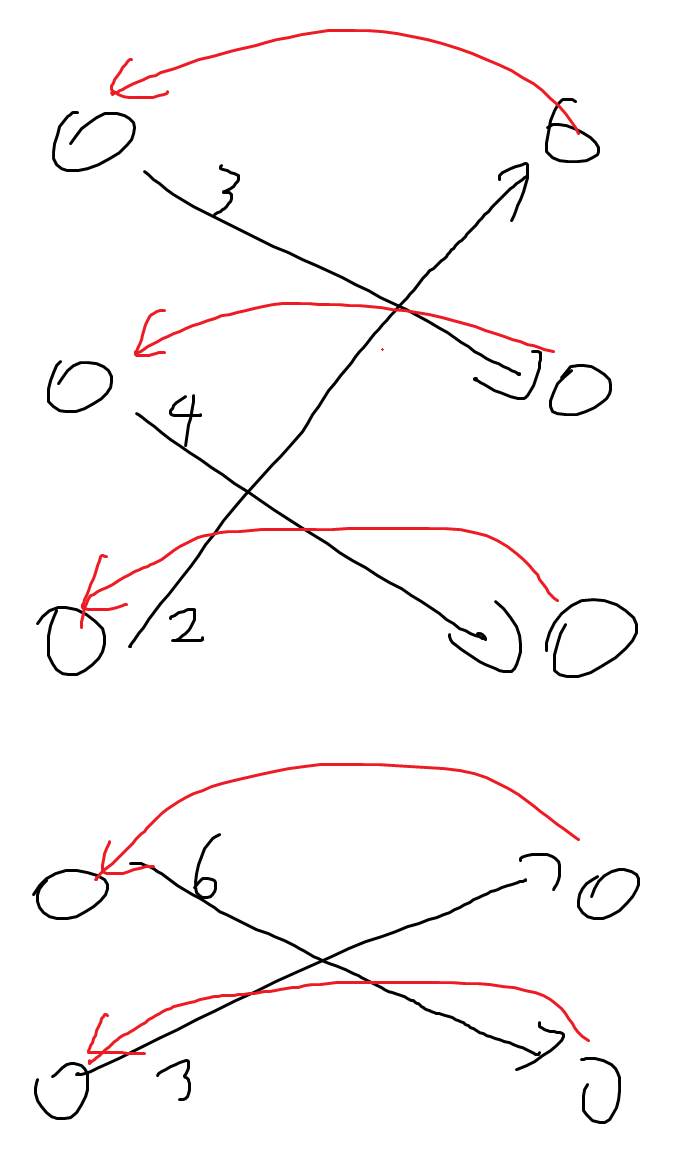
예제는 이런 형태의 그래프입니다.

각각의 사이클마다 그 사이클에서 흐를 수 있는 유량은 (정점에서 나가는 간선의 용량) + (정점으로 들어가는 간선의 용량)보다 작거나 같습니다. 따라서 소스에서 각 정점으로 $in + out$ 만큼의 유량을 보낸 다음, 싱크로 내보낼 수 있는 유량을 전부 빼내고 남은 유량들을 사이클에서 돌린다고 생각해도 됩니다.
유량이 사이클에 머물러 있다는 것은 $L(u)$와 $R(u)$를 동시에 지난다는 뜻이므로, 위 사진에서 빨간 간선에 흐르는 유량을 최소화하면 된다는 것을 알 수 있습니다.

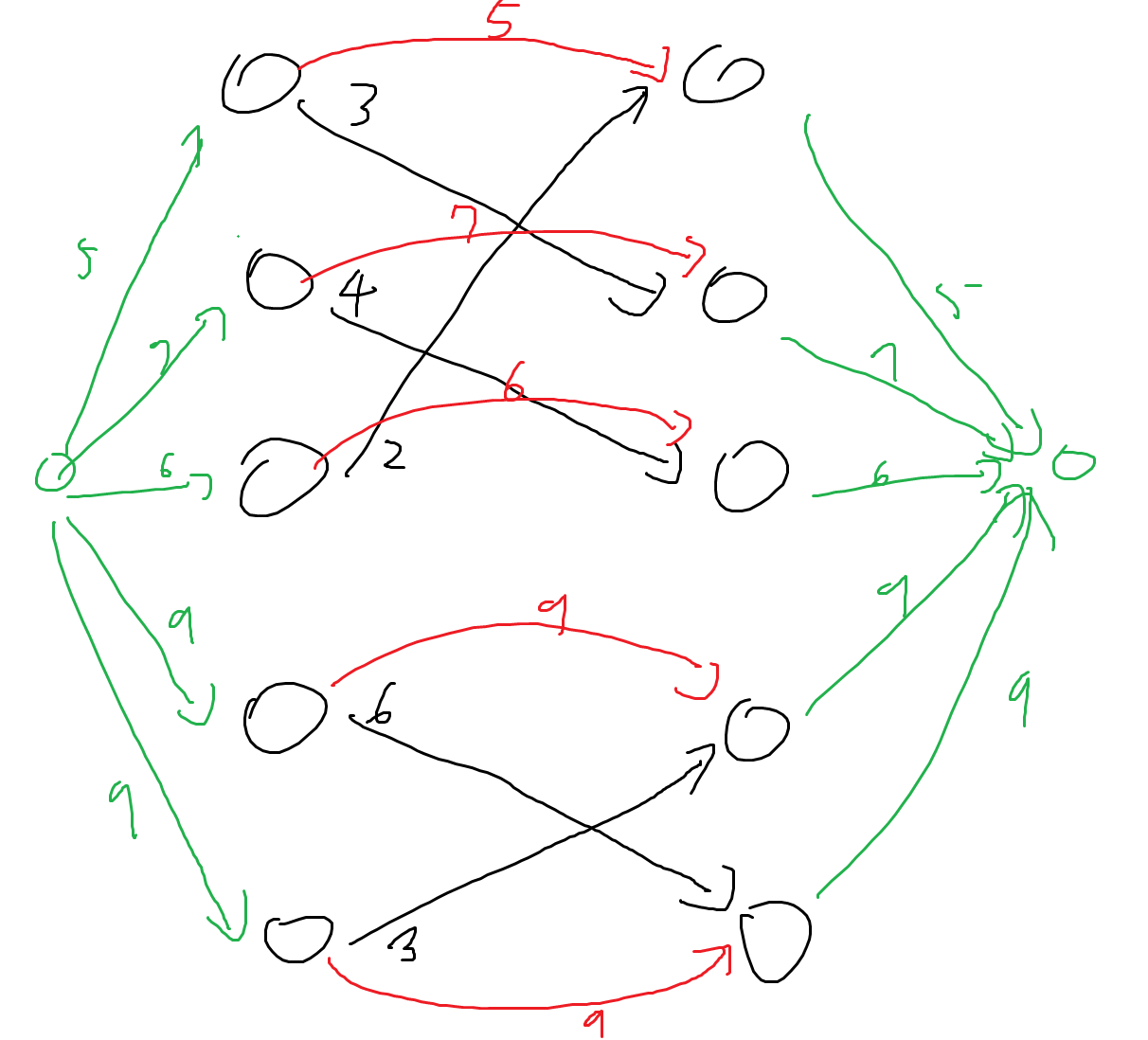
따라서 이런 식으로 그래프를 만든 다음, 빨간색 간선의 비용을 1로 설정해서 MCMF를 돌리면 문제를 해결할 수 있습니다.

전체 코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int N, M, In[2020], Out[2020], R;
CostScalingMCMF<4040, int, int, 0x3f3f3f3f, 0x3f3f3f3f> G;

int main(){
    ios_base::sync_with_stdio(false); cin.tie(nullptr);
    cin >> N >> M;
    int S = 0, T = N + N + 1;
    for(int i=1; i<=M; i++){
        int u, v, w; cin >> u >> v >> w;
        G.addEdge(u, N+v, w, 0);
        Out[u] += w; In[v] += w;
    }
    for(int i=1; i<=N; i++){
        G.addEdge(S, i, In[i] + Out[i], 0);
        G.addEdge(N+i, T, In[i] + Out[i], 0);
        G.addEdge(i, N+i, In[i] + Out[i], 1);
        G.addEdge(N+i, i, In[i] + Out[i], 0);
    }

    for(int i=1; i<=N; i++) R += In[i] + Out[i];
    R -= G.run(T+1, S, T).second;
    cout << R;
}