2021 KOI 1차대회 고등부 문제 풀이

총평 및 문제 감상

이제 대학생이라 KOI에 참가하지 못하지만, 그래도 제가 한동안 정말 열심히 준비했던 대회인 만큼 풀이는 지속적으로 작성할 생각입니다.

작년에 비해 1교시 난이도는 상승한 것 같습니다. 11번까지는 예년보다 크게 어렵지 않지만, 비버 챌린지 난이도가 꽤 많이 상승한 것 같습니다. Nim Game(혹은 Sprague-Grundy Theorem), Burnside’s Lemma, Slope Trick처럼 어려운 개념을 활용하는 문제가 작년보다 증가했습니다. 특히 작년에는 간단한 Nim Game만 출제되었지만 올해는 Sprague-Grundy Number가 직접적으로 출제되었다는 점이 인상적입니다. Nim Game이 2년 연속으로 나왔다는 점에 주목해야 할 것 같습니다.

1교시 8/9번처럼 과거 지역 예선(2017년 이전 대회)에서 자주 나왔던 유형의 문제들도 조금씩 보입니다. 2017년 이전 지역 예선 문제를 구해서 공부하는 것도 KOI 1차 대회를 준비하는데 도움이 될 것 같습니다. 1교시 12번 문제처럼 일명 “노가다 문제”라고 부르는 문제들을 어떻게 처리할지 대회 전략을 짜는 것도 중요해 보입니다. (저는 일단 넘어가고 남는 시간에 시도합니다.)

비버챌린지 유형의 문제가 특히 인상적입니다. 2019/2020년과 다르게 비버 챌린지에도 서브태스크가 적용되었습니다.
“정답이 존재한다” 또는 “이 전략이 최적이다”를 증명할 수 있는 풀이(정해)와 대회 중에 빠르게 풀 수 있는 속칭 야매 풀이가 많이 다른 문제가 몇 개 있습니다. 야매 풀이를 잘 찾기 위해서는 많은 문제를 풀어봐야 합니다. 개인적으로 비버챌린지 기출로 대비하는 것보다는 온라인 저지 사이트에서 다양한 문제를 많이 풀어보는 것을 추천합니다. 비버 챌린지 유형이라고는 하지만, 실제로 비버 챌린지에 출제되는 문제보다 알고리즘 지식과 사고력을 훨씬 많이 요구하기 때문에 온라인 저지 사이트에서 다양한 문제를 풀어보는 것이 좋을 것입니다.

2교시 실기 문제 난이도는 2019년보다는 확실히 쉽고, 2020년과 비교했을 때도 2번을 제외하면 많이 쉬워진 느낌입니다. 2019/2020 문제와는 다르게 올해 2/3번 문제에서 Codeforces 느낌이 많이 나네요. 이 점도 다음 대회를 준비할 때 고려하면 좋을 것 같습니다.

2교시 실기 문제는 아직 검증되지 않은 코드입니다. 풀이에서 언급한 로직을 구현하긴 했지만, 코딩 미스로 인해 틀렸을 가능성이 있는 코드이니 양해 부탁드립니다. 온라인 저지에 문제가 올라오면 채점을 받은 뒤 검증된 코드로 수정할 예정입니다.

문제 유형

문제	유형	문제	유형	문제	유형	문제	유형
1번	경우의 수	2번	DP	3번	경우의 수	4번	경우의 수
5번	Nim Game	6번	경우의 수 Burnside’s Lemma	7번	함수/정수론	8번	ad-hoc
9번	ad-hoc	10번	ad-hoc	11번	DP	12번	DP
13번	DP/휴리스틱	14번	시뮬레이션	15번	위상정렬	16번	BFS
17번	DP/Slope Trick	18번	Sprague-Grundy	19번	휴리스틱	20번	ad-hoc
1번	수학/이분탐색
2번	수학/그리디
3번	투포인터/누적합

1-1. 상금 배분 (8점)

A가 $a$번, B가 $b$번 이기는 경우의 수는 $f(a, b) = \begin{cases} {a+b-3 \choose b} & a = 4 \ {a+b-3 \choose b-1} & a \geq 2, b = 4 \end{cases}$로 계산할 수 있습니다. 또한 각 경우의 수가 발생하는 확률은 $p(a, b) = 1 / 2^{a+b-2}$로 계산할 수 있습니다.

(A가 이기는 횟수, B가 이기는 횟수)로 가능한 모든 순서쌍과 경우의 수, 확률을 나열해봅시다.

	경우의 수	확률
(4, 0)	1C0 = 1	1 * 1/4 = 4/16
(4, 1)	2C1 = 2	2 * 1/8 = 4/16
(4, 2)	3C2 = 3	3 * 1/16 = 3/16
(4, 3)	4C3 = 4	4 * 1/32 = 2/16
(2, 4)	3C3 = 1	1 * 1/16 = 1/16
(3, 4)	4C3 = 4	4 * 1/32 = 2/16

A가 4번 이길 확률은 $13/16$이고, B가 4번 이길 확률은 $3/16$입니다. 그러므로 정답은 13억원이 됩니다.

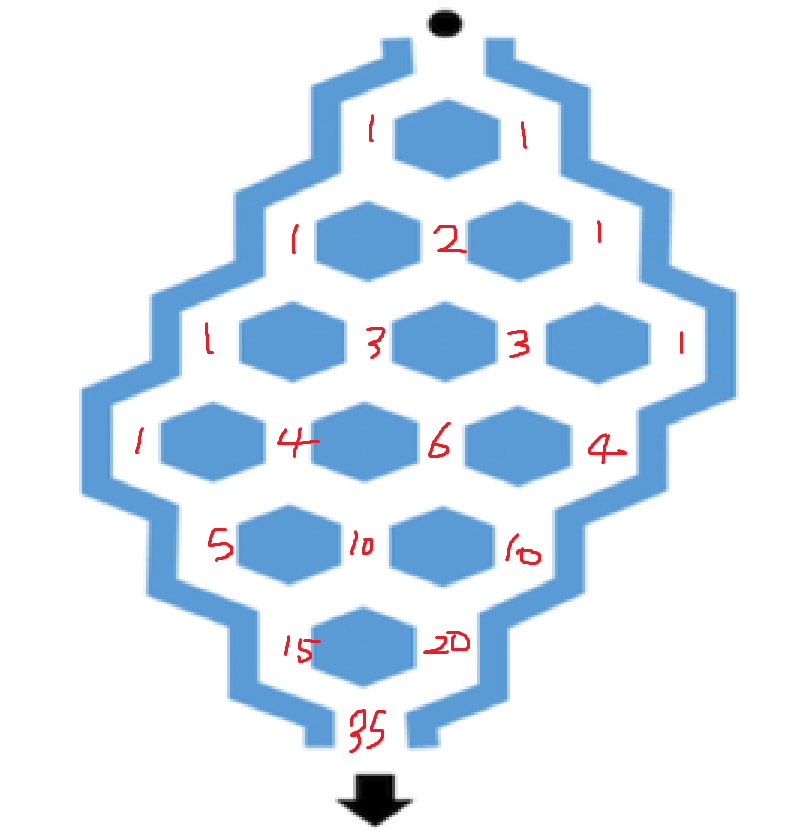
1-2. 구슬 경로의 수 (8점)

손으로 DP를 계산하면 됩니다.

정답은 35입니다.

1-3. 동전과 확률 (8점)

동전을 2개 뒤집는 경우의 수는 ${10 \choose 2} = \frac{90}{2}$이고, 뒷면이 모두 A인 경우의 수는 ${x \choose 2} = \frac{x^2-x}{2}$입니다.
$\frac{x^2-x}{90} \leq \frac{4}{10}, x(x-1) \leq 36$을 만족하는 가장 큰 자연수 $x$는 6입니다.

1-4. 발표 순서 (8점)

문자열의 Prefix를 고정시킨 뒤, 그 Prefix로 시작하는 문자열의 개수를 구하면 쉽게 해결할 수 있습니다.

Axxxxx : 120가지 / 누적 120
Bxxxxx : 120가지 / 누적 240
CAxxxx : 24가지 / 누적 264
CBADEF : 1가지 / 누적 265

정답은 265입니다.

1-5. 돌 무더기 게임 (9점)

전형적인 Nim Game입니다. 각 덩어리에 있는 돌의 개수를 xor했을 때 0이라면 항상 후공이 이기는 전략이 존재하고, 0이 아니라면 항상 선공이 이기는 전략이 존재합니다.
1, 2, 3을 xor하면 0이기 때문에 항상 B가 이기는 전략이 존재합니다.

1-6. 직소 퍼즐 (9점)

전형적인 Burnside’s Lemma 문제입니다. 작년에 Algoshitpo 팀 블로그에서 Burnside’s Lemma 튜토리얼을 작성했으니 참고하시면 됩니다.

$c(k) = 2^{\text{gcd}(k, 6)}$이라고 하면 정답은 $\displaystyle \frac{1}{6} \sum_{k=1}^{6} c(k) = 84/6 = 14$입니다.

1-7. 삼각형 위의 격자점 (9점)

삼각형의 각 변을 선분으로 생각합시다. 선분의 한쪽 끝점을 $(0, 0)$으로 옮기면 $y = \frac{b}{a}x, (0 < x < k)$와 같이 $x$좌표 범위가 제한된 일차함수라고 생각할 수 있습니다. $x$가 정수일 때 $bx$가 $a$의 배수가 되는 경우의 수를 세면 됩니다. 꼭짓점은 따로 생각하는 것이 편합니다.

$\overline{AB} : y = \frac{29}{155}x, (0 < x < 155)$ : 0개
$\overline{BC} : y = \frac{5}{7}x, (0 < x < 210)$ : 29개
$\overline{CA} : y = \frac{11}{5}x, (0 < x < 55)$ : 10개
꼭짓점 : 3개

정답은 42개입니다.

1-8. 숫자 추측 (9점)

일단 가능한 경우의 수를 모두 나열해봅시다.

(1, 1) : 합 2 곱 1
(1, 2) : 합 3 곱 2
(1, 3) : 합 4 곱 3
(1, 4) : 합 5 곱 4
(2, 2) : 합 4 곱 4
(2, 3) : 합 5 곱 6
(2, 4) : 합 6 곱 8
(3, 3) : 합 6 곱 9
(3, 4) : 합 7 곱 12
(4, 4) : 합 8 곱 16

다래는 두 수 $a, b$의 곱을 알고 있는 사람입니다. $ab$를 알고 있을 때 $a, b$의 값을 모른다면 $ab$는 4입니다.
나은은 두 수 $a, b$의 합을 알고 있는 사람입니다. $a+b$를 알고 있을 때 $a, b$의 값을 모른다면 $a+b$는 4 5 6 중 하나입니다.

다래가 나은에게 $ab$가 4라는 정보를 제공했기 때문에, $ab$와 $a+b$를 모두 알고 있는 나은은 $a, b$의 값을 알 수 있습니다. 하지만 다래는 $a+b$가 4 5 6 중 하나라는 정보를 알고 있어도 (1, 4), (2, 2) 중 어떤 것이 답인지 알지 못합니다.

다래가 $a \neq b$라는 정보를 얻고 나면 $a, b$가 각각 1, 4라는 것을 알게 됩니다. 정답은 17입니다.

1-9. 항아리 (10점)

각 행동 별로 $b, w$가 어떻게 변화하는지 생각해봅시다.

검은 돌 2개를 꺼낸 경우 : $(b, w) \rightarrow (b-1, w)$
흰 돌 2개를 꺼낸 경우 : $(b, w) \rightarrow (b+1, w-2)$
1개씩 꺼낸 경우 : $(b, w) \rightarrow (b-1, w)$

문제 지문에서는 무작위로 돌을 꺼낸다고 하지만, 결과가 한 개로 정해져 있기 때문에 원하는 순서대로 돌을 꺼내도 무방합니다. (2)를 이용해 흰색 돌을 최대한 많이 없앤 뒤, (1)과 (3)을 이용해 검은색 돌을 모두 없애는 전략을 사용할 것입니다.

만약 $w$가 짝수라면, (2)를 이용해 흰 돌을 모두 없앨 수 있습니다. 그 다음 (1)을 이용해 검은 돌을 한 개만 남길 수 있습니다.
만약 $w$가 홀수라면, (2)를 이용해 흰 돌을 한 개만 남길 수 있습니다. 그 다음 (3)을 이용해 검은 돌을 모두 없앨 수 있습니다.

$\text{jug}(10, 34), \text{jug}(45, 5), \text{jug}(100, 111)$은 각각 B, W, W입니다.

1-10. 중심 노드 찾기 (10점)

The Celebrity Problem으로 잘 알려진 문제입니다.

2명의 사람 $a, b$를 임의로 선택해서 $\text{query}(a, b)$를 호출합시다. 만약 반환값이 yes라면 $a$는 중심 노드가 될 수 없습니다. 만약 반환값이 no라면 $b$는 중심 노드가 될 수 없습니다.

(상한) 쿼리 1번으로 후보 해를 최소 1개 이상 제거할 수 있으므로 최악의 경우 $n-1$번의 쿼리를 통해 중심 노드를 찾을 수 있습니다.
(하한) 쿼리 1번으로 최대 1개의 후보 해를 제거할 수 있기 때문에 하한도 $n-1$이 됩니다.

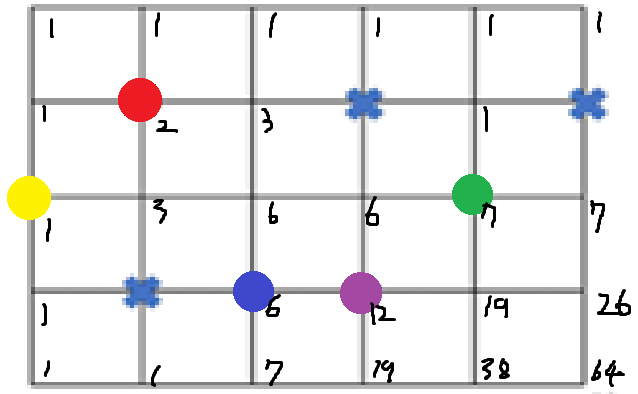
1-11. 두 번 이상 지나는 경로 찾기 (10점)

여사건을 생각합시다. 전체 경우의 수에서 0번 / 1번 지나는 경로의 개수를 제거하면 됩니다.

전체 경우의 수는 64가지입니다. 0번 지나는 경로는 존재하지 않고, 1번 지나는 경로는 11개 존재합니다.
구체적으로,

빨간색 점만 지나는 경로 : 0개
노란색 점만 지나는 경로 : 1개
초록색 점만 지나는 경로 : 6개 (출발 → 초록 2가지, 초록 → 도착 3가지)
파란색 점만 지나는 경로 : 1개
보라색 점만 지나는 경로 : 3개 (출발 → 보라 1가지, 보라 → 도착 3가지)

정답은 64 - 11 = 53입니다.

1-12. 사각형 세기 (10점)

정답은 30이니 다른 문제를 모두 풀고 남는 시간 동안 열심히 찾으면 됩니다.

1-13. 첫 월급 (9점)

$D[i] := $ 선물 상자 $i$개를 구매하는 최소 비용이라고 정의하면 점화식은 $D[i] = \min(D[i-1]+175, D[i-3]+400, D[i-5]+700)$이 됩니다. 점화식을 계산하고 역추적을 하면 1, 3, 3, 3개 구매하는 것이 최적임을 알 수 있습니다.

또는 선물 상자를 1, 3, 5개 구매할 때 개당 175, 133.33, 140원이라는 것을 이용해 효율이 좋은 상품을 많이 구매하는 휴리스틱을 사용해도 됩니다.

1-14. 하노이의 탑 (9점)

횟수를 최소화할 필요는 없으므로 자유롭게 하면 됩니다.

1-15. 2등을 찾아라! (9점)

위상 정렬을 생각해봅시다.
어떤 정점 $v$가 2등이 될 수 있다는 것은, 위상 정렬을 했을 때 $v$가 2번째로 오는 경우가 존재하는 것을 의미합니다.

1일차에는 모든 정점이 2등이 될 수 있습니다.

1/2/8은 각각 5/3/4 바로 다음에 오면 2등이 됩니다.
나머지 다른 정점들은 임의의 in-degree가 0인 정점 다음에 나오면 2등이 될 수 있습니다.

2일차에는 1, 3, 4, 5, 6이 2등이 될 수 있습니다.

7은 3, 2가 항상 먼저 나와야 하기 때문에 2등이 될 수 없습니다.
2는 3, 4보다 나중에 나와야 하기 때문에 2등이 될 수 없습니다.
8은 3, 5보다 나중에 나와야 하기 때문에 2등이 될 수 없습니다.
1/6은 3 다음에 오면 2등이 됩니다.
3/4/5는 임의의 in-degree가 0인 정점 다음에 나오면 2등이 될 수 있습니다.

3일차에는 3, 5만 2등이 될 수 있습니다.

4는 무조건 1등입니다.
1/6은 4, 3보다 나중에 나와야 하기 때문에 2등이 될 수 없습니다.
3/5는 4 다음에 오면 2등이 됩니다.

4일차에는 3만 2등이 될 수 있습니다.

5는 4, 3보다 나중에 나와야 하기 때문에 2등이 될 수 없습니다.
3은 4 다음에 오면 2등이 됩니다.

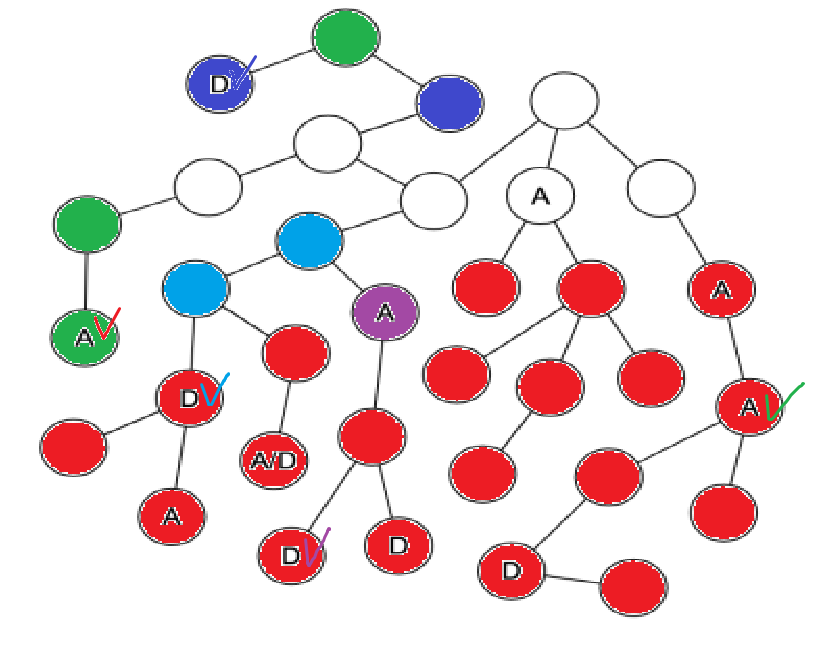
1-16. 천사와 악마 (12점)

손으로 BFS를 직접 시뮬레이션 한다고 생각합시다.
천사가 살고 있는 정점과 7 이상 떨어져 있는 정점을 모두 제거합시다. 빨간색 체크가 되어 있는 정점과 7 이상 떨어져 있는 정점은 빨간색으로, 초록색 체크가 되어 있는 정점과 7 이상 떨어져 있는 정점은 초록색으로 색칠했습니다.
마찬가지로 악마가 살고 있는 정점과 2 이하로 떨어져 있는 정점을 모두 제거합시다. 하늘색, 파란색, 보라색으로 표시했습니다.

색칠되지 않은 정점이 정답입니다.

1-17. 단조증가 수열 (12점)

$D(i, j) := $ $A_1, A_2, \cdots , A_i$를 단조 증가 수열로 만들고, $A_i = j$가 되도록 하는 최소 횟수라고 정의합시다. 수가 커질수록 +를 눌러야 하는 횟수가 크게 증가하므로 $j$는 14 이하라고 생각해도 충분합니다.

점화식은 $D(i, j) = \min(D(i-1, j-1), D(i-1, j-2), \cdots , D(i-1, 1)) + \vert A_i - j \vert$가 됩니다. $8 \cdot 14$ 크기의 DP Table을 직접 채우고 최적해를 역추적하면 문제를 풀 수 있습니다.

컴퓨터를 이용해서 이런 점화식을 계산할 때 Slope Trick을 이용하면 $O(NX)$를 $O(N \log N)$으로 최적화할 수 있습니다. 관심 있는 분들은 한 번 공부해보세요. ($N$: 원소 개수, $X$: 수 범위)

1-18. 삼각형 게임 (13점)

점이 $n$개 있을 때 선분을 하나 그리면 점이 각각 $a$개 있는 게임과 $n-a-2$개 있는 게임으로 나뉘게 됩니다. 자신이 선분을 그리는 것으로 인해 모든 게임을 점이 1개인 게임으로 만들 수 있다면 승리할 수 있습니다.

$G(1) = 0$이므로 Sprague-Grundy Theorem을 이용하는 문제라는 것은 쉽게 알 수 있습니다. Grundy Number를 잘 구해봅시다.

$G(0) = 0$
$G(1) = 0$
$G(2) = 1 = \text{mex}(G(0) \bigoplus G(0)) = \text{mex}(0)$
$G(3) = 1 = \text{mex}(G(0) \bigoplus G(1)) = \text{mex}(0)$
$G(4) = 2 = \text{mex}(G(0) \bigoplus G(2), G(1) \bigoplus G(1)) = \text{mex}(1, 0)$
$G(5) = 0 = \text{mex}(G(0) \bigoplus G(3), G(1) \bigoplus G(2)) = \text{mex}(1, 1)$
$G(6) = 3 = \text{mex}(G(0) \bigoplus G(4), G(1) \bigoplus G(3), G(2) \bigoplus G(2)) = \text{mex}(2, 1, 0)$
$G(7) = 1 = \text{mex}(G(0) \bigoplus G(5), G(1) \bigoplus G(4), G(2) \bigoplus G(3)) = \text{mex}(0, 2, 0)$
$G(8) = 1 = \text{mex}(G(0) \bigoplus G(6), G(1) \bigoplus G(5), G(2) \bigoplus G(4), G(3) \bigoplus G(3)) = \text{mex}(3, 0, 3, 0)$
$G(9) = 0 = \text{mex}(G(0) \bigoplus G(7), G(1) \bigoplus G(6), G(2) \bigoplus G(5), G(3) \bigoplus G(4)) = \text{mex}(1, 3, 1, 3)$
$G(10) = 3 = \text{mex}(G(0) \bigoplus G(8), G(1) \bigoplus G(7), G(2) \bigoplus G(6), G(3) \bigoplus G(5), G(4) \bigoplus G(4)) = \text{mex}(1, 1, 2, 1, 0)$
$G(11) = 3 = \text{mex}(G(0) \bigoplus G(9), G(1) \bigoplus G(8), G(2) \bigoplus G(7), G(3) \bigoplus G(6), G(4) \bigoplus G(5)) = \text{mex}(0, 1, 0, 2, 2)$
$G(12) = 2 = \text{mex}(G(0) \bigoplus G(10), G(1) \bigoplus G(9), G(2) \bigoplus G(8), G(3) \bigoplus G(7), G(4) \bigoplus G(6), G(5) \bigoplus G(5)) = \text{mex}(3, 0, 0, 0, 1, 0)$
$G(13) = 2 = \text{mex}(G(0) \bigoplus G(11), G(1) \bigoplus G(10), G(2) \bigoplus G(9), G(3) \bigoplus G(8), G(4) \bigoplus G(7), G(5) \bigoplus G(6)) = \text{mex}(3, 3, 1, 0, 3, 3)$

$G(13) \neq 0$이므로 플레이어가 항상 승리하는 필승법이 존재합니다. 게임 판의 상태(모든 게임의 Grundy Number를 xor한 결과)가 0이 되도록 만들어주면 됩니다.
첫 번째 턴에 게임을 (3, 8)로 쪼개면 됩니다. ($G(3) \bigoplus G(8) = 1 \bigoplus 1 = 0$)

1-19. 팀 구성 (14점)

문제를 보자마자 정말 막막하다는 생각이 듭니다. 사각형 세기와 더불어 가장 마지막에 푸는 것을 추천합니다.
정답을 구하는 과정을 소개하면 너무 길어지기 때문에, 시도해볼만한 전략만 몇 가지 소개하고 넘어가겠습니다. 정답은 KOI 공식 답지의 29-32페이지를 참고하세요.

탐색해야 할 후보가 너무 많기 때문에, 적당한 전략을 활용해 탐색 범위를 줄이는 것이 중요합니다.

인접한 0 이상의 수들은 한 그룹으로 묶을 수 있습니다.
리프 노드가 음수라면 그 리프 노드를 제거해도 됩니다. (ex. 중앙 상단에 있는 -1)
음수를 뚫고 들어갔을 때 이득을 볼 수 있다면 뚫고 들어갑니다. (ex. 우측 하단에서 -1을 뚫고 들어가면 1, 1, 2를 먹을 수 있습니다.)
리프 노드부터 시작해 적당한 양수 서브 트리를 묶으면 편합니다. (ex. 우측 상단에 있는 5, 1, -5)

1-20. 2행 정렬 (14점)

적절히 swap해서 아래처럼 만든 다음, $(1, 1), (2, 2), \cdots , (15, 15)$를 바꿔주면 됩니다.

-1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 -15
 1  2  3  4  5  6  7  8  9  10  11  12  13  14  15

2-1. 야구 시즌 (100점)

같은 지역 리그에 있는 팀끼리 $A$번, 다른 지역 리그에 있는 팀끼리 $B$번 경기를 하면 총 $f(A, B) = A \cdot N \cdot \frac{M \cdot (M-1)}{2} + B \cdot \frac{NM \cdot (NM-M)}{2} = $ $ANM(M-1)/2 + BNM^2(N-1)/2$번 경기를 진행합니다.

$A = kB$라고 두면, $f(kB, B) \leq D$를 만족하는 가장 큰 자연수 $B$를 찾는 문제가 되고, 변수가 하나이므로 이분 탐색(파라메트릭 서치)을 이용해 $O(\log D)$만에 정답을 구할 수 있습니다.

$KBNM(M-1)/2 + BNM^2(N-1)/2 \leq D$를 잘 정리해서 $B \leq \frac{2D}{NM(K(M-1)+M(N-1))}$로 바꾸면 $O(1)$에 계산할 수도 있습니다.

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

ll N, M, K, D;

ll Check(ll B){
    ll A = K * B;
    ll t1 = M * (M-1) / 2 * A * N;
    ll t2 = N*M * (N*M - M) / 2 * B;
    return t1 + t2;
}

void Solve(){
    cin >> N >> M >> K >> D;
    ll l = 1, r = 1e9;
    while(l < r){
        ll m = l + r + 1 >> 1;
        if(Check(m) <= D) l = m;
        else r = m - 1;
    }
    if(ll res=Check(l); res <= D) cout << res << "\n";
    else cout << "-1\n";
}

int main(){
    ios_base::sync_with_stdio(false); cin.tie(nullptr);
    int T; cin >> T;
    while(T--) Solve();
}

2-2. 초직사각형 (100점)

주어지는 카드의 $T_i$가 모두 A라고 가정해봅시다. $U_i$가 큰 것부터 사용하는 것이 그리디가 성립한다는 것을 직관적으로 알 수 있습니다. 이때 사용한 카드들의 $U_i$를 $U_1 \geq U_2 \geq \cdots \geq U_K$이라고 하면, $U_i$를 사용했을 때 부피의 증가율이 $\frac{A_0 + \sum_{j=1}^{i} U_j}{A_0 +\sum_{j=1}^{i-1} U_j}$이라는 것을 알 수 있습니다.

이 풀이를 확장시키면 만점 풀이를 얻을 수 있습니다. 주어진 카드들을 $T_i$에 따라 분류하면, 각 그룹 별로 증가율을 독립적으로 계산할 수 있습니다. 그러므로 각 그룹 별로 $U_i$에 대해 내림차순으로 정렬하고 전부 모아서 증가율이 큰 카드부터 사용하면 됩니다.
분수의 분자/분모가 각각 $2 \cdot 10^{11}$ 정도까지 커질 수 있으므로, 분수를 비교할 때 __int128_t를 사용해야 합니다.

#include <bits/stdc++.h>
#define all(v) v.begin(), v.end()
using namespace std;
using ll = long long;
using LL = __int128_t;

int N, K;
vector<ll> V[4];
vector<ll> S[4];

struct Card{
    int id, idx;
    Card(){}
    Card(int id, int idx) : id(id), idx(idx) {}
};

bool operator > (const Card &a, const Card &b){
    LL a1 = S[a.id][a.idx], a2 = S[a.id][a.idx-1];
    LL b1 = S[b.id][b.idx], b2 = S[b.id][b.idx-1];
    return a1*b2 > b1*a2;
}

int main(){
    ios_base::sync_with_stdio(false); cin.tie(nullptr);
    cin >> N >> K;
    for(int i=0,t; i<4; i++) cin >> t, V[i].push_back(t);
    for(int i=1; i<=N; i++){
        char T; ll U; cin >> T >> U;
        V[T-'A'].push_back(U);
    }

    for(int i=0; i<4; i++){
        sort(1+ all(V[i]), greater<>());
        S[i].resize(V[i].size());
        partial_sum(all(V[i]), S[i].begin());
    }

    vector<Card> cards;
    for(int i=0; i<4; i++){
        for(int j=1; j<V[i].size(); j++) cards.emplace_back(i, j);
    }
    sort(all(cards), greater<>());
    cards.resize(K);
    for(auto [id,idx] : cards) cout << char('A' + id) << " " << V[id][idx] << "\n";
}

2-3. 공통 부분 수열 확장 (100점)

어떤 문자열 $S$의 $i$번째 문자부터 $j-1$번째 문자로 구성된 부분 문자열을 $S[i:j]$라고 정의합시다. 반 열린 구간 $[i, j)$라고 생각하면 됩니다.

문자열 $W$가 확장 가능하다는 것은 어떤 수 $k(0 \leq k \leq \vert W \vert)$와 문자 $c$가 있어서, $W[0:k] + c + W[k:\vert W\vert]$가 $X, Y$의 공통 부분 수열이 된다는 것을 의미합니다. 이러한 $k, c$가 존재하는지 빠르게 알아내야 합니다.

$W$의 접두사(Prefix) $W[0:j]$가 $X$의 접두사 $X[0:i]$의 부분 수열이 되는 가장 작은 $i$을 $\text{PreX}[j]$라고 합시다.
$W$의 접미사(Suffix) $W[j:\vert W \vert]$가 $X$의 접미사 $X[i:\vert W \vert]$의 부분 수열이 되는 가장 큰 $i$를 $\text{SufX}[j]$라고 합시다.
$\text{PreY}[j], \text{SufY}[j]$도 비슷하게 정의할 수 있습니다.

어떤 수 $k$와 어떤 수 $c$에 대해 $W$를 $W[0:k] + c + W[k:\vert W\vert]$로 확장 가능하다는 것은, $X[\text{PreX}[k]:\text{SufX}[k]]$과 $Y[\text{PreY}[k]:\text{SufY}[k]]$가 각각 $c$를 포함하고 있다는 것과 동치입니다.

$\text{PreX}, \text{SufX}, \text{PreY}, \text{SufY}$는 투포인터를 이용해 $O(\vert X \vert + \vert Y \vert)$ 시간에 전처리할 수 있습니다. $X[i:j]$에 어떤 문자 $c$가 존재하는지 확인하는 것은 누적합(Prefix Sum)을 이용하면 $O(\vert X \vert)$ 전처리를 통해 $O(1)$ 시간에 확인할 수 있습니다.

그러므로 문제를 $O(\vert X \vert + \vert Y \vert)$에 해결할 수 있습니다.

#include <bits/stdc++.h>
#define all(v) v.begin(), v.end()
using namespace std;

int N, M, K;
string X, Y, W;
vector<int> PreX, SufX, PreY, SufY;
array<vector<int>,26> PosX, PosY;

void Clear(){
    PreX.clear(); SufX.clear();
    PreY.clear(); SufY.clear();
    for(int i=0; i<26; i++) PosX[i].clear(), PosY[i].clear();
}

void Resize(){
    N = X.size(); M = Y.size(); K = W.size();
    PreX.resize(K); SufX.resize(K);
    PreY.resize(K); SufY.resize(K);
    for(int i=0; i<26; i++) PosX[i].resize(N), PosY[i].resize(M);
}

void PreCalc(const string &S, vector<int> &Pre, vector<int> &Suf, array<vector<int>,26> &Pos){
    for(int i=0, j=0; i<S.size(); i++) if(S[i] == W[j]) Pre[j++] = i;
    for(int i=S.size()-1, j=W.size()-1; i>=0; i--) if(S[i] == W[j]) Suf[j--] = i;
    for(int i=0; i<S.size(); i++){
        Pos[S[i]-'a'][i] = 1;
    }
    for(int i=0; i<26; i++) partial_sum(all(Pos[i]), Pos[i].begin());
}

bool Exist(int flag, int ch, int s, int e){
    if(s > e) return false;
    array<vector<int>,26> &Pos = flag ? PosY : PosX;
    return Pos[ch][e] - (s ? Pos[ch][s-1] : 0) > 0;
}

bool Check(int s0, int e0, int s1, int e1){
    if(s0 > e0 || s1 > e1) return false;
    for(int i=0; i<26; i++){
        if(Exist(0, i, s0, e0) && Exist(1, i, s1, e1)) return true;
    }
    return false;
}

void Solve(){
    Clear();
    cin >> X >> Y >> W;
    Resize();
    PreCalc(X, PreX, SufX, PosX);
    PreCalc(Y, PreY, SufY, PosY);

    int flag = 0;
    flag |= Check(0, SufX[0]-1, 0, SufY[0]-1);
    for(int i=0; i+1<K; i++){
        flag |= Check(PreX[i]+1, SufX[i+1]-1, PreY[i]+1, SufY[i+1]-1);
    }
    flag |= Check(PreX[K-1]+1, N-1, PreY[K-1]+1, M-1);
    cout << flag << "\n";
}

int main(){
    ios_base::sync_with_stdio(false); cin.tie(nullptr);
    int T; cin >> T;
    while(T--) Solve();
}