백준5401 Escape from the Minefield

작성일 | In

문제 링크

  • https://icpc.me/5401

문제 출처

  • 2003 BAPC C번

사용 알고리즘

  • 들로네 삼각분할

시간복잡도

  • $O(N \log N)$

풀이

풀이는 그림 한 장으로 요약할 수 있습니다.

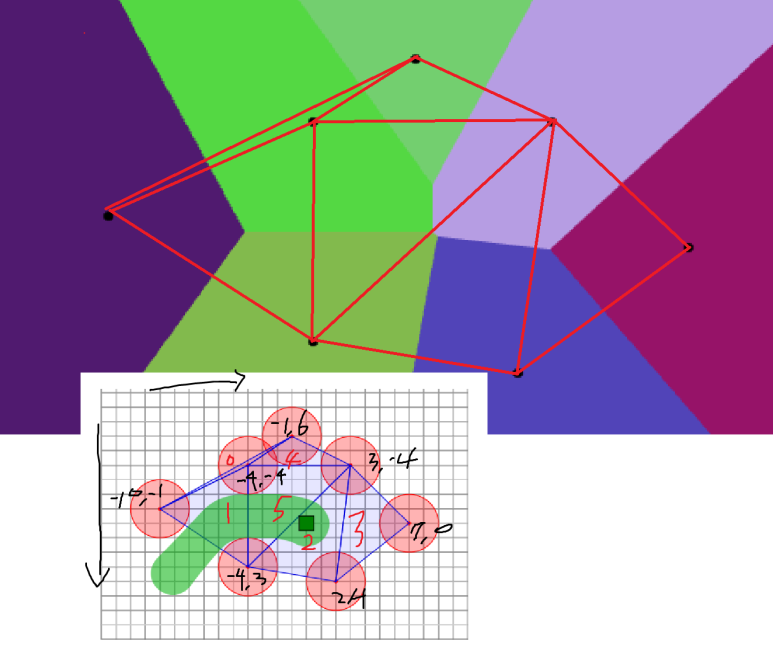
결국 $O(N \log N)$ 시간에 들로네 삼각분할을 구할 수 있다면, 삼각 분할에 있는 간선들을 길이가 긴 순서대로 보면서 시작 지점 $P(0, 0)$과 outer face가 연결될 때까지 간선을 제거하면 됩니다.

전체 코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
double Solve(){
    /// delaunay triangulation
    int N; cin >> N;
    vector<P> V(N);
    for(auto &i : V) cin >> i.x >> i.y;

    double res = 1e18;
    for(const auto &p : V) res = min(res, hypot(p.x, p.y));
    if(N <= 2) return res;

    shuffle(all(V), random_device());
    const auto triangles = triangulate(V);

    /// get arcs in triangulation
    vector<pair<P,P>> arcs;
    for(const auto &[a,b,c] : triangles){
        arcs.emplace_back(a, b);
        arcs.emplace_back(a, c);
        arcs.emplace_back(b, c);
    }
    compress(arcs);

    /// get faces adjacent to arc
    int st = -1, outer = triangles.size();
    vector<vector<int>> faces(arcs.size());
    for(int i=0; i<triangles.size(); i++){
        const auto &[a,b,c] = triangles[i];
        if(InTriangle(P(0,0), a, b, c)) st = i;
        vector<pair<P,P>> edges = { make_pair(a,b), make_pair(a,c), make_pair(b,c) };
        for(const auto &e : edges) faces[IDX(arcs, e)].push_back(i);
    }

    /// get dual graph of delaunay triangulation
    vector<tuple<double,int,int>> vec;
    for(int i=0; i<arcs.size(); i++){
        if(faces[i].empty()) continue;
        if(faces[i].size() == 1) faces[i].push_back(outer);
        vec.emplace_back(Dist(arcs[i].first, arcs[i].second) / 2, faces[i][0], faces[i][1]);
    }

    if(st != -1){
        vector<int> par(triangles.size()+1);
        iota(all(par), 0);
        function<int(int)> find = [&](int v){ return v == par[v] ? v : par[v] = find(par[v]); };
        function<void(int,int)> merge = [&](int u, int v){ if(find(u) != find(v)) par[find(u)] = find(v); };
        sort(vec.rbegin(), vec.rend());
        for(const auto &[x,s,e] : vec){
            if(find(st) == find(outer)) break;
            merge(s, e);
            res = min(res, x);
        }
    }
    for(auto i : use) delete i; use.clear();
    return res;
}